PROPOSITIO VI

63 Si in sphaera plures circuli fuerint signati, qui per centrum sphaerae transierit omnibus erit maior; reliquorum autem, hi quidem, quorum longitudo a centro aequalis fuerit, erunt aequales; at cuius longitudo maior fuerit, erit minor.

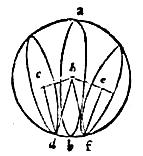
64 In sphaera ab, cuius centrum h, circulus quidem ab per centrum h transeat, circuli autem cd ef extra centrum: aio iam quod circulus ab maior erit reliquis et, si circulorum cd ef longitudo a centro h fuerit eadem, ipsi cd ef circuli erunt aequales; ille autem, cuius longitudo fueri[n]t maior, erit minor. 65 A centro enim h ducam perpendiculares hc he ad circulos cd ef, eruntque per corollarium primae huius c e talium circulorum centra et ipsae perpendiculares longitudines circulorum a centro sphaerae per diffinitionem. 66 Capiam autem puncta quaelibet d f in periferiis talium circulorum et ducam rectas cd ef dh fh. Eruntque triangula hcd hef habentia rectos angulos ce. Quare linea hd longior quam linea dc, quoniam angulo recto opponitur; sed dh est semidiameter sphaerae et ideo aequalis semidiametro ab circuli per sphaerae centrum transeuntis. 67 Maior igitur semidiameter circuli ab semidiametro cd circuli cd et maior ergo erit circulus ab circulo cd et similiter maior ostendetur circulus ab circulo ef, quod est primum. 68 Si autem ponantur hc he longitudines aequales, tunc earum quadrata aequalia erunt, quae ablata a quadratis hd hf aequalibus relinquent quadrata cd ef linearum aequalia. 69 Igitur et ipsae lineae cd cf aequales erunt, et ipsi tunc circuli cd ef aequales., quod est secundum. 70 Demum si ipsarum hc he longitudinum altera, utpote he, ponatur maior, tunc quadratum he maius erit quam quadrato hc et ideo, facta iam dicta quadratorum subtractione, supererit quadratum ef minus quadrato cd. 71 Quare linea ef minor erit quam linea cd et per consequens circulus ef minor circulo cd, quod est tertium ex demonstrandis.