PROPOSITIO V
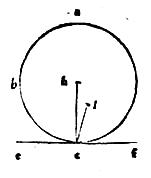
57 Si sphaeram plana superficies contingat, a puncto autem contactus2 recta linea ad contingentem superficiem perpendiculariter inter sphaeram ducatur, in eadem centrum sphaerae esse necesse est.
58 Sphaeram abc tangat plana superficies in puncto c, a quo educatur recta ch tangenti plano perpendicularis: aio quod ch linea ibit per sphaerae abc centrum. 59 Nam si centrum [S:2r] non sit in recta ch continuata, sit ergo extra ipsam, utpote in puncto l. 60 Et coniungatur recta cl, eritque per praecedentem lc recta perpendicularis plano tangenti. 61 Sed per hypothesim, linea hc eidem plano perpendicularis est: duae igitur rectae hc lc eidem plano et in idem punctum perpendiculares sunt, quod per 13 undecimi est impossibile. 62 Non erit ergo sphaerae abc centrum nisi in linea ch continuata, quod est propositum.