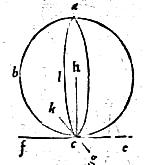
PROPOSITIO IIII

49 Sphaeram plana superficie contingente, si a puncto contactus ad centrum sphaerae sphaerae recta linea ducatur, necesse est eam supra superficiem contingentem stare perpendiculariter.

50 Sphaeram abc contingat plana superficies in puncto c (in uno enim puncto tanget per praecedentem). A centro autem sphaerae, quod sit h, in punctum contactus c recta linea hc ducatur. 51 Aio quod hc linea tangenti plano perpendicularis est. 52 Ducam enim per rectam hc duo plana secantia sphaeram. Eruntque, per primam huius, factae in sphaera sectiones circuli, quorum commune centrum h per primam partem corollarii eiusdem et communis semidiameter hc. 53 Sint autem communes sectiones planorum circularium cum plano tangente ecf gck, quae cum sint in plano tangente, ibunt iam extra sphaeram et perinde extra circulos abc adc. 54 Itaque recta ef tanget circulum abc in puncto c et recta gk tanget circulum adc in puncto eodem c, cum utraque harum rectarum sit in plano circuli quem tangit. 55 Quare linea hc a centro h ad contactum c ducta per 17 tertii Euclidis perpendicularis erit tam ad lineam ef quam ad lineam gk. 56 Igitur, per 4 undecimi, recta hc perpendicularis erit ad planum, in quo iacent lineae ef gk, quod est ipsum planum tangens sphaeram. Et hoc fuit demonstrandum.