PROPOSITIO III

41 Si sphaeram plana superficie[n]s contingat, in uno tantum puncto contingere necesse est.

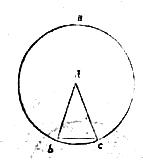
42 Tangat enim, si possibile est, plana superficies sphaeram abc in pluribus punctis quam uno, utpote in punctis b c. 43 Et centrum sphaerae per praemissam inventum sit d et coniungantur rectae bc cd db. 44 Eritque, per diffinitionem sphaerae, triangulum bcd isosceles, habens scilicet duo latera bd dc a centro ad superficiem sphaerae aequalia. 45 Omnis autem alia linea a puncto d protracta ad rectam bc brevior erit ipsis bd dc singulis et perinde cadet intra superficiem sphaerae. 46 Omnis enim linea exiens a centro sphaerae brevior eius semidiametro cadit intra superficiem sphaerae. Quam ob rem tota linea bc cadet intra superficiem sphaerae. 47 Sed cum planum tangens sphaeram, in quo iacet linea bc, sit extra superficiem sphaerae, iam eadem linea bc cadet extra superficiem sphaerae, quod est impossibile. Reliquit ergo propositum.

48 Unde manifestum est quod signatis duobus punctis in superficie sphaerae linea recta coniungens signata puncta cadit intra superficiem sphaerae.