PROPOSITIO II

25 Sphaerae propositae centrum invenire.

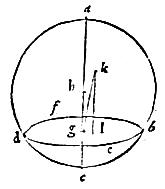
[S:1v] Sit proposita sphaera abd: oportet eius centrum reperire. 26 Secabo sphaeram abcd plano quolibet. Sitque plani secantis ac sphaericae superficiei communis sectio periferia bcdf, quae per praecedentem erit circulus. 27 Circuli itaque bed centrum per primam tertii Euclidis inventum sit g, a quo excitetur per secundam undecimi linea agc circulo perpendicularis, utrinque ad sphaerae superficiem producta, quae per decimam primi per aequalia dividatur in puncto h. 28 Aio itaque quod h punctum est centum sphaerae. 29 Nam si aliud sit sphaerae centrum, aut erit in linea ac aut extra eam. 30 Si in linea ac, tunc secabitur per aequalia in ipso centro, per diffinitionem sphaerae. 31 Verum secatur per aequa in puncto h, quod esset impossibile. 32 Si autem centrum sphaerae sit extra lineam ac, tunc aut erit in superficie circuli bed aut extra eam. 33 Si in superficie circuli bed, tunc per primam partem corollarii praemiss<a>e illud erit centrum circuli bed. 34 Igitur circulus bed habebit duo centra, quod est rursus impossibile. 35 Si extra superficiem circuli bed, tunc sit ipsum k, a quo per 11 undecimi Euclidis ducam perpendicularem lineam kl ad superficiem circuli bed. 36 Quae si cadat in punctum g, tunc duae perpendiculares plano bed in idem punctum coi<n>cident, quod per 13 undecimi est impossibile. 37 Si autem alio cadat, ut in punctum l, tunc per 2 partem corollariipraemiss<a>e, punctum l centrum erit circuli bed. 38 Sed eius centrum fuit g, quod denique est impossibile. 39 Non est ergo sphaerae abc centrum aliud quam h punctum, quod proponebat inveniendum.

40 COROLLARIUM

Manifestum igitur ex hac est quod si a centro cuiuslibet circuli in sphaera signati linea perpendicularis ad eius superficiem educatur utrinque ad sphaericam usque superficiem, necesse est eam per centrum ipsius sphaerae transire.