PROPOSITIO XXXIII
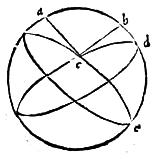
237 In sphaerae superficie puncto signato, si ab eo in alicuius circuli in eadem sphaera descripti periferiam plures quam duae rectae lineae ductae fuerint aequales, punctum illud polum eiusdem circuli esse necesse est.
238 A puncto a in superficie sphaerae ad periferiam circuli bcd agatur tres rectae ab ac ad, quae ponantur aequales: aio tunc quod a punctum polus est circuli bcd. 239 Ducam enim a puncto a ad circulum bcd perpendicularem lineam ae et coniungam rectas be ce de. Eruntque in triangulis abe ace ade anguli apud e recti, latus autem ae commune. 240 Quare per penultimam primi elementorum Euclidis, si quadratum ae auferatur a quadratis ab ac ad per hypothesim aequalibus, supererunt quadrata be ce de aequalia, unde et ipsae lineae be ce de erunt inter se aequales et idcirco per 9 tertii Euclidis e punctum erit centrum circuli bcd. 241 Verum linea ea perpendicularis est circulo bcd: igitur per 10 huius a punctum polus est talis circuli, quod est propositum.