43 Adhuc colorum talium in iride generatorum causa [S:56] potest ex magnitudine spacii242 stillicidia comprehendentis, et ex raritate243 aut densitate stillicidiorum coargui244.

44 Huius demonstrationis causa245, in descriptione praecedentis imaginari possum246 infinitos circulos se invicem in punctis ak247 secantes, ultra scilicet citraque circulum afk. Sed exempli gratia, hinc et inde binos assumo, videlicet248 apk, aqk249 ulteriores, et ark, ask citeriores circulos, quos singulos radius solaris250 medius nfk251 secet252 in punctis pqrs253. 45 // Sicut igitur in praecedenti fecimus quinque radiales terminos a punctis dmnoe254 deductos in puncto f se invicem secantes, et255 in periferiam circuli afk cadentes, atque cum lineis visualibus a puncto a256 aequalem angulum ipsi akf semper servantes. 46 Ita et257 in unoquoque circulorum apk, aqk, ark, ask id258 idem facere hic possumus, ut radii totidem259 ab ipsis punctis dm[C:44r]noe260 deducantur secantes se in puncto p et in periferiam apk cadentes, item totidem ab iisdem quinque punctis per punctum q transmissos, et in periferiam aqk terminatos. 47 Item similiter totidem tam per punctum261 r quam per punctum s262 traiectos et in ipsorum ark, ask circulorum periferias263 deductos. 48 // Sic enim264 servabitur ubique anguli akf, qui265 est recti dimidium aequalitas, quod reflexionis ratio postulat, ut per 25am266 suamque additam267 constint268. // Nec refert utrum circuli apk, aqk, ark, ask sint aequales circulo afk, modo269 se invicem secent in punctis a, k aut in locis non sensibiliter inde remotis. 49 // Hoc pacto dispositio colorum270, quae per praemissam271 in periferia272 afk facta est, hic in caeteris273 quatuor274 circulis apk275, akq276, ark [A:12v] et277 ask repetetur278. Et coloratio per multum stillicidiorum spacium279 generata roborabitur. // Et tale spacium280 intra circulos deductos281, ultra citraque k punctum claudetur, quantum282 angulorum reflexionis aequalitas intra stillicidiorum regionem servari poterit. 50 // Itaque cum k punctum sit medium inter zonas colorum iridis, ut patuit283 in praemissa284, habeatque superne viridem et285 croceum colores, et inferne ceruleum286 et ruffum287, causaque talis diversitatis assignata sit ex quantitate288 lucis solaris in stillicidia infusae; id289 idem hic com[S:57]probari poterit ex magnitudine intervalli stillicidia recipientis. // 51 Siquidem cum duae sint colorationis causae, altera scilicet activa et exhibens, altera passiva et recipiens; illa scilicet solaris lux, haec autem multiplex irroratio, iam ad demonstrationem [C:44v] argumentum utrinque sumendum est290. 52 // Sicut291 ergo duae colorum zonae, quarum limes est k punctum, propter moderatiorem solis lucem, sortitae sunt magis sobrios colores, viridem scilicet et ceruleum292, ita et hic id idem accidet293 propter angustius stillicidiorum294 intervallum iuxta k punctum, quo circuli tale295 intervallum claudentes in angustum coeunt. 53 // Itemque sicut duae sequentes supra et infra praedictas positae colorum zonae, propter maiorem luminis copiam, luminosiorem colorem receperunt, croceum scilicet et rubrum296, ita et hic id idem fiet propter amplius stillicidiorum intervallum, circulis a puncto k in latum digredientibus. 54 // Dictum est praeterea quod interiores zonae sortitae sunt colores magis saturos et ebrios, quoniam297 minor ambitus coadunat magis vim coloris. Unde duarum mediarum zonarum interior ceruleum298, exterior viridem recepit299. Ex duabus300 autem extremis intima ruffum301, extima croceum adepta est. 55 // Quod si rursum conferre velis exteriores zonas cum mediis, hoc est, croceam302 cum viridi303, et hinc rubram304 cum cerulea305, poteris argumentum sumere densitate ac raritate306 stillicidiorum. Nam extremi radii obliquius307 incidentes circulorum periferiis incurrunt crebriora stillicidia, et propterea308 efficacius colorant309, quam medii, qui rectius incidentes paucioribus occurunt310 guttis. // Sic quam optime potuimus, colorum causas311 reddidimus, et a sole et a stillicidiis. [C:45r]
Scholium
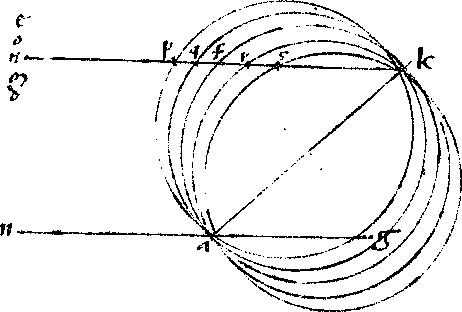
56 Notandum quod demonstrationes 27ae312 , 29ae313 et praesentis additionis intelligendae sunt per totum ambitum iridis. Hoc pacto, cum per corollarium314 25ae315 centrum solis, centrum visus, quod est a, centrumque iridis semper sint316 in eadem recta linea, sit talis recta linea nag317, ita ut n318 intelligatur centrum solis, a centrum visus, g vero centrum iridis, quae recta merito vocabitur axis iridis. 57 Itaque stante axe nag319, imaginemur circumduci planum totum, in quo descripti sunt circuli afk, cum reliquis, circumduci inquam per integram revolutionem. Sic enim tali conversione k320 feretur321 per medium cingulum iridis, hoc est describet mediocrem iridis circulum, qui duas colorum zonas habet intra, et totidem extra. // Ita hoc pacto [S:58] demonstratio322 facta in 27a323, 29a324 et in praesenti additione intelligetur per totum iridis ambitum, circumducta iam descriptione per totum ambitum.