21
91 Proposita sphaerae diametro, quinque corporum regularium ab ipsa sphaera comprehensorum latera exponere, et invicem conferre.
Esto sphaerae datae diametros ab quae secetur in puncto c per aequalia et descripto super ea semicirculo, sit ad dupla ipsius db et excitentur perpendiculares ce, df et connectant af, be, fb. Et sic procede. Quoniam ab sesquialtera est ipsius ad. 92 Ideo per 8am et 17am Sexti, quadratum ipsius ab sesquialterum est ad quadratum ipsius af ergo, per 16am huius, af latus est pyramidis in sphaera proposita clausi. Item quoniam ab tripla est ipsius bd ideo per 8am et 17am Sexti, quadratum ipsius ab triplum est ad quadratum ipsius bf.
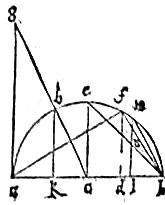
Itaque, per 18am huius, bf latus erit cubi, in proposita sphaera descripti. Adhuc, quoniam per penultimam Primi, quadratum ipsius ab duplum est ad quadratum ipsius be. Ideo, per 17am huius, be latus erit octahedri in ipsa sphaera constituti.
Item ponatur ipsi ab perpendicularis et aequalis ag et acta gc secundae periferiam in puncto h ducatur hk perpendicularis ad ab. 93 Et quoniam ga ipsius ac dupla est, ideo propter triangulorum similitudinem hk dupla est ipsius kc ergo quadratum ipsius hk ad quadratum kc quadruplum. Quare, per penultimam Primi, quadratum ipsius hc vel cb quincuplum ad quadratum ipsius kc. Item tota ab totius bc dupla, et abscisa ad abscisae db dupla. Ergo relicta db dupla est relictae dc per 19am Quinti. 94 Sic bc tripla ipsius cd. Quare quadratum ipsius cb nonuplum est ad quadratum ipsius cd et ideo ck maior, quam cd. Sit ergo ipsi ck aequalis cl et excitata perpendiculari lm connectatur mb eritque lb aequalis ipsi ak et kl aequalis ipsi lm quoniam scilicet utraque dupla est ipsius kc. Quoniam itaque quadratum ipsius bc quincuplum est ad quadratum ipsius ck. Ideo et quadratum ipsius ab quincuplum erit ad quadratum ipsius kl quoniam scilicet, sicut simplum ad simplum, sic duplum ad duplum. 95 Igitur per 19am huius, kl et ei aequalis lm est latus hexagoni, vel semidiameter circuli circumscribentis pentagona basim anguli solidi icosahedri. Et ak lb sunt latera decagoni eiusdem circuli. Quare per penultimam Primi et 13am huius ml erit latus pentagoni eiusdem circuli, quod et ipsum per 19am huius, est latus icosahedri. Tandem secetur fb latus cubi secundum extremam [S:121] et mediam rationem in puncto n cuius maius segmentum bn per praecedentis corollarium erit latus dodecahedri in eadem sphaera locati. 96 Et quia quadratum ipsius ad quadruplum est ad quadratum ipsum db et quadratum ipsius bf triplum ad quadratum ipsius db per 8am et 17am Sexti. Ideo ad maior, quam bf et eo magis al quam bf. Sed al in puncto k per 11am huius bf vero in puncto n per hypothesim, extrema et media ratione secatur. Ergo, per 7am huius, kl et ideo lm maior, quam bn et eo magis bm maior, quam bn hoc est icosahedri latus maius, quam dodecahedri latus. 97 Inventa sunt ergo latera quinque corporum regularium a data sphaera comprehensorum et simul ostensum, quod maximum latus est af pyramidis, proximum in magnitudine latus be octahedri. Tertio dein loco latus bf cubi. Post haec latus bm icosahedri, ut patet per arcus assumptos. Sed bm maius quam bn esse dudum ostendimus. Quare bn latus dodecahedri minimum.