F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Euclidis regularia solida Liber decimustertius 20
<- App. -> <- = ->

20

82 Dodecahedrum construere, et data sphaera comprehendere et ostendere quod dodecahedri latus irrationale est, et appellatur apotome si rationalis fuerit sphaerae diametros.

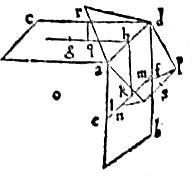
Duarum basium cubi contiguarum ab, ac latera duo ad et db. Cum opposito secentur singula per aequalia in punctis hfe ductisque ef, gh, hk per centra basium gk. 83 Secentur ipsae gh, ke, kf singulae secundum mediam extremamque rationem, in punctis q, l, m suntque maiora segmenta gq, kl, km quibus singulis aequales sint singulae perpendiculares qr quidem ad planum ac ipsae autem ln, mp ad planum ab. Connexisque punctis a, n, p, d, r fiet pentagonum aequilaterum et aequiangulum.

Quod enim sit aequilaterum, sic patet.

figura 21

quadrato  an graffa aperta quadrato  al graffa aperta quadrato ke vel ae graffa chiusa per 4am huius graffa aperta quadrato graffa chiusa kl vel ln
quadrato  el quadrato
          quadrato
quadrato ln
quadrato ln
Ergo al dupla ipsius kl quare aequalis ipsi lm et ideo ipsi np. Et similiter ostendemus, quod dp ipsi np quodque ar, rd singulae sunt ipsis an, dp singulis aequales.

Quod autem totum pentagonum ardpn sit in uno plano, sic patet.

Exeat ks ipsis ln, kp parallelus et ideo eisdem aequalis et plano ab perpendicularis. Eritque sicut rq ad ipsam qh, sic hk ad ipsam ks. 84 Nam in linea secta extrema et media ratione, sic est tota ad maius, sicut maius ad minus segmentum. Ergo triangula rqh, hks sunt similia et quia sunt in uno plano, et latera rq, hk. Item ipsa qh, ks sunt aequidistantia. Ideo per 30am Sexti, linea rhs est una recta. Quare per 2am Undecimi rhs et ahd rectae sunt in uno plano et pentagonum ipsum in uno plano.

85 Quod vero sit aequiangulum, sic constat.

Cum ek sit secta in puncto l secundum mediam et extremam rationem et km sit aequalis kl maiori segmento: ideo per 5am huius, ipsa quoque em in puncto k similiter secta est et maius segmentum ek. Unde sic argue. [S:119]

quadrato  ap graffa aperta quadrato  mp   vel mk graffa chiusa per 4am huius graffa aperta quadrato graffa chiusa ek vel ae
quadrato am graffa aperta quadrato  em quadrato
      quadrato
quadrato  ae
quadrato  ae
Ergo quadratum ap quadruplum ad quadratum ae et ideo ap dupla est ipsius ae. Et perinde aequalis lateri cubi ad. 86 Similiter ostendemus quod dn aequalis est eidem ad. Quare per 8am Primi, tam angulus anp quam angulus npd aequalis est angulo ard. Estque pentagonum aequilaterum sicut dudum fuit demonstratum. Igitur per 9am huius, pentagonum anpdr aequiangulum est. Non aliter super unumquodque reliquorum undecim laterum cubi comparetur pentagonum. Itaque duodecim pentagona component dodecahedrum.

87 Et circumscribitur ab eadem sphaera, a qua et cubus. Quod sic demonstratur.

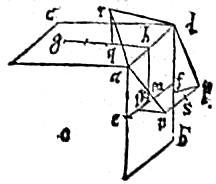
figura 22

Duo plana per rectas hk, ef secent cubum quorum planorum communis sectio sit ipsa recta ok quae secabitur a diametro cubi et secabat vicissim eam per aequalia in centro cubi, per 40am Undecimi. Sit itaque o centrum cubi. Et sic argumentare. In primis lineae oa, od aequales, quoniam semidiametri sunt tam cubi, quam sphaerae, per 40am Undecimi et 18am huius, et quoniam ok ipsi ek, et ks ipsi km sunt aequales, ideo os in puncto k secatur extrema et media ratione. Unde sic procede.

quadrato  op graffa aperta quadrato  ps vel sk graffa chiusa per 4am huius graffa aperta quadrato graffa chiusa ok vel ae
  quadrato
quadrato os quadrato
88 Ergo quadratum ipsius op triplum est ad quadratum ipsius ae. Sed ae dimidium est lateris cubi. Igitur per 18am potestatem od semidiameter est sphaerae. Et similiter ostendemus, quod a puncto o rectae universae ad reliquos angulos dodecahedri sunt semidiametri sphaerae cubum circumscribentis. 89 Cumque octo ex angulis dodecahedri sint simul cum angulis cubi, sicut qui ad ipsa a d puncta: patet quod sphaera ipsa, quae cubum, circumscribet dodecahedrum. Quod tandem latus ipsum dodecahedri sit apotome, sic patet.

Agatur rp quae secabit ipsam ad secundum extremam et mediam rationem per 10am huius. 90 Et maius segmentum erit ipsi ar aequale: cumque adsit potentia rationalis (quoniam sphaerae diameter rationalis) ideo [S:120] ar latus dodecahedri, per 8am huius, erit apotome.

Unde manifestum est, quod cubi latere, in sphaera quapiam clausi, extrema et media ratione diviso; maius segmentum est dodecahedri in eadem sphaera constituti latus.

Inizio della pagina
 ->