21.^a

Trianguli, cuius data sunt latera, dabuntur et anguli.

Ut si trianguli abc latera singula data sint: aio quod eius anguli dabuntur. 29 Dabitur enim, per 10^am huius, perpendicularis cd. Datur ergo ratio ac ad cd. Sed sicut ac ad cd sic sinus totus ad sinum anguli a, hoc est sinum arcus ab angulo a assumpti: tantus est enim angulus, quantus arcus, quem angulus in centro constitutus assumit. Itaque cum quatuor proportionalium magnitudinum scilicet ac, cd sinus totus et sinus anguli a tres datae sint: iam, per 7^am huius, reliqua, scilicet sinus anguli a dabitur: et ideo ipsae angulus a in tabula sinuum, per sex praemissas, constructa, dabitur. 30 Similiter et angulus b per latus bc et cd perpendicularem notescet, unde et reliquus angulus bca datus veniet.

22.^a

Trianguli, cuius dantur anguli, datur proportio laterum.

Nam si datur angulus a datur eius sinus: scilicet sicut sinus totus ad sinum anguli a sic ac ad cd: datur ergo ratio²⁵ ac ad cd. Item similiter dabitur ratio bc ad cd. Quare ratio laterum bc, ca dabitur. Item angulus acd est complementum anguli a quoniam cum eo conficit angulum rectum: et ideo datus. 31 Et similiter angulus bcd complementum ipsius b anguli datur. Hinc ergo, ut prius, dabitur ratio ca ad ad necnon [A:10r] ratio cb ad bd. Et ideo ratio tam ipsius ac quam ipsius bc ad ipsum ab datur. Similiter in omnibus triangulis te expedies, quamvis perpendicularis cadat extra triangulum: nam tunc per angulum obtusum intrinsecum, sumitur extrinsecus acutus. Sed in triangulis orthogoniis, ipsa rectum angulum comprehendentia latera sunt pro kathetis. Et opus est facilius.

23.^a

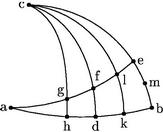
32 In triangulis sphaeralibus, ex datis lateribus dantur anguli et ex datis angulis dantur latera.

In unica descriptione complectar trianguli orthogonii sphaeralis data: nam ex orthogonio sequuntur praecepta reliquorum triangulorum. Sint ergo in superficie sphaerae quadrantes circulorum maiorum ab, bc angulum b rectum continentes. Quo fit ut c punctum sit polus ipsius ab circuli; et a punctum ipsius bc vicissim polus. 33 A quibus polis ad ipsos circulos rursum quadrantes descendant cd, ae se vicissim in puncto f secantes. Item a polo c alii duo quadrantes utrinque ab ipso cd descendant cgh, clk qui secent quartas ae, ab in punctis g, h, k, l²⁶. Atque ut praeceptorum fundamentum melius intelligatur, ita hos quadrantes disponam: ut sinus arcus cf sit medius proportionalis inter sinum totum et sinum arcus ce. Et etiam inter sinum arcus cg et sinum arcus cl. Quare fiet, sicut sinus totus ad sinum arcus cg sic sinus arcus cl ad sinum arcus ce. Quibus suppositis, haec sequuntur. 34 Aggregatum ipsorum arcuum fa, ad erit quadrans: et ipsi arcus in maxima differentia. Et sinus arcus cf aequalis sinui anguli afd item arcus fg, dk aequales inter se. Et ipsi arcus fl, dh inter se aequales. Unde et ipsi ag, kb arcus aequales invicem: et ipsi ah, le arcus aequales erunt invicem. Item sinus arcus cg erit et sinus anguli alk. [A:10v] Et e contrario, sinus arcus cl erit et sinus anguli agh. Adhuc secto per medium arcu be in puncto M ratio sinus aggregati arcuum ga, ah ad sinum differentiae eorundem arcuum, erit sicut quadratum sinus arcus cM ad quadratum sinus arcus Mb. 35 Eandemque rationem habebit sinus aggregati arcuum la, ak ad sinum differentiae eorumdem: et eandem sinus aggregati arcuum fa, ad ad sinum eorum differentiae. Et similiter in omni triangulo sphaerali orthogonio inter quadrantes ae, ab constituto. Sicut igitur ipsorum arcuum fa, ad aggregati sinus maximus est, quia scilicet sinus quadrantis ac semidiameter sphaerae: sic et ipsorum arcuum fa, ad maxima est differentiarum, quae in reliquis triangulis orthogoniis inter quartas ae, ab positis.