Data Sphaeralium Triangulorum

36 Nunc his iactis fundamentis, veniam ad explicationem datorum.

p.^a

In triangulo igitur agh datis arcubus, dabuntur anguli.

Nam datorum arcuum dantur sinus. Et sicut sinus arcus ae hoc est sicut sinus totus ad sinum arcus eb sic sinus arcus ag ad sinum arcus gh. Scilicet tria ex his dantur, scilicet sinus arcus ag sinus arcus gh sinusque totus: igitur et quartum scilicet sinus arcus eb qui est sinus anguli a dabitur: et iam ipse angulus a dabitur. Similiter per arcus ga, ah dabitur angulus agh.

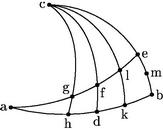
2.^a

37 Item datis duobus arcubus ag, gh dabitur reliquus ah.

Nam sic dantur talium arcuum complementa, quae sunt cg, ge. Scilicet sicut est sinus arcus cg ad sinum arcus ge sic sinus totus ad sinum arcus hb. Igitur dabitur sinus arcus hb et ipse arcus hb et eius complementum ah.

3.^a

38 Item dato arcu ag et angulo a dantur reliqui arcus et anguli.

Nam sinus anguli a est ipse sinus arcus eb. Scilicet sicut est sinus totus ad sinum arcus eb sic sinus arcus ag ad sinum arcus gh. 39 Igitur sinus arcus gh et ipse arcus gh datur. Et inde reliqua.

4.^a

Item datis arcubus ga, ah datur reliquus gh et anguli.

Nam ga est aequalis kb et arcus [A:11r] ah aequalis arcui le. Sed sicut est sinus arcus kb ad sinum totum, sic est sinus arcus le ad sinum arcus lc. Igitur sinus arcus lc et ipse arcus lc qui est quantitas anguli agh dabitur. Sicut autem sinus arcus hb ad sinum totum, sic sinus arcus ge ad sinum arcus gc. Scilicet tria ex his nota, cum arcus ge, hb sint complementa arcuum ga et ah datorum, igitur arcus gc et eius complementum gh dabitur.

5.^a

Item datis arcubus ah, gh dabitur arcus reliquus ag.

40 Dantur enim ipsorum ah, hg complementa, scilicet arcus hb, gc scilicet sicut sinus totus ad sinum arcus hb sic sinus arcus gc ad sinum arcus ge. Igitur sinus arcus ge et ipse arcus ge datur: quare et eius complementum ag arcus datur.

6.^a

Item datis angulo a et arcu gh dantur reliqui arcus et anguli.

Nam quantitas anguli a est ipse arcus eb. Scilicet sicut sinus arcus eb ad sinum totum, sic sinus arcus gh²⁷ ad sinum arcus ag. Igitur sinus arcus ag et ipse arcus ag datur, et reliqua ut prius.

7.^a

41 Item datis angulis a et agh acutis dabuntur et arcus singuli.

Nam quantitas anguli a est arcus eb et quantitas anguli agh est arcus lc datur igitur arcus lc et arcus ce complementum ipsius eb. Sed sicut sinus arcus lc ad sinum arcus ce, sic sinus totus ad sinum anguli cle. Igitur datur sinus anguli cle et ipse angulus cle ipsique oppositus angulus alk. Sed quantitas anguli alk est arcus cg. 42 Itaque datur arcus cg et eius complementum arcus gh. Et inde reliqui, ut ante. Vel sic. Quoniam sicut sinus arcus eb ad sinum totum sic sinus arcus lk ad sinum arcus la. Ideo dabitur sinus arcus la et ipse arcus la et eius complementum le arcus, et ipsi le aequalis arcus ah. Et inde reliqui, ut ante.

8.^a

Item dato angulo a et arcu ah dantur reliqua.

43 Nam arcus ah est aequalis arcui le datur ergo arcus le et eius complementum arcus al. Scilicet sicut sinus totus ad sinum arcus eb, qui est quantitas anguli a [A:11v] sic sinus arcus al ad sinum arcus lk dabitur ergo arcus lk et eius complementum, arcus cl, qui est quantitas anguli agh. Datur ergo angulus agh. Ergo et coetera, ut prius, in duobus praemissis datis.

9.^a

Item datis arcu gh et angulo agh, dantur reliqua.

44 Nam sic datur arcus cg et complementum ipsius gh, datur et arcus cl quantitas ipsius anguli agh. Sed sicut sinus totus ad sinum arcus cg, sic sinus arcus cl ad sinum arcus ce, dabitur ergo sinus arcus ce et ipse arcus ce eiusque complementum eb, qui est quantitas anguli a. Igitur per 5^um vel 6^um datum dabuntur coetera.

10.^a

Item dato angulo a et aggregato arcuum ga, ah tamquam uno arcu: dabuntur singuli arcus et anguli.

45 Nam sicut est quadratum sinus arcus cM ad quadratum sinus arcus Mb, sic est sinus arcus aggregati ex arcubus ga, ah ad sinum arcus differentiae eorundem: quare cum tria data sint, dabitur sinus arcus dictae differentiae, et ipse arcus. Cum itaque arcuum ga, ah aggregatum et differentia datae sint: dabuntur arcus ga, ah singuli et reliqui per antedicta.

46 Vel sic quoniam sicut est aggregatum sinus totus et sinus complementi anguli dati a ad differentiam eorumdem sinuum, sic est sinus arcus aggregati ex arcubus ga, ah ad sinum arcus differentiae eorumdem: et horum tria data sunt: propterea dabitur quartum scilicet sinus arcus dictae differentiae, et ipse arcus differentiae. Quare cum et aggregatum et differentia nunc arcuum ga, ah data sint: dabuntur arcus ga, ah singuli per se, et coetera per superiora praecepta.

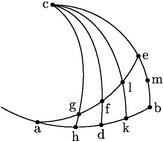
11.^a

47 Eodem modo in triangulo afd maximae differentiae cum arcus aggregatus ex arcubus fa, ad sit quadrans, dabitur ipsa differentia.

Vel sic, quoniam sinus totus, sinus arcus cf et sinus arcus ce sint continue proportionales: et duo ex his [A:12r] extrema data sint: dabitur, per 6^am huius medium, scilicet sinus arcus cf et ipse arcus cf eiusque complementum fd et hinc per 6^a horum datorum, arcus²⁸ singuli fa, ad.

48 Item complura data resolvuntur per tabellam foecundam Ioannis Regiomontani: multa per tabellam nostram beneficam, quae omnia latius demonstrata sunt et a Menelao, et a nobis in duobus nostris Sphaericorum libellis. Et eorum executio practica per Canones tabularum Ioannis memorati, ac Tabulae magnae primi mobilis, et in libellis problematum nostrorum explanatur.

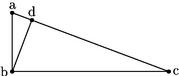
49 Ut autem intelligamus artificium tam foecundae, quam beneficae, atque etiam sinus recti tabellarum, sit triangulum abc cuius angulus abc rectus: et bd perpendicularis, ad latus ac in quo linea ab est sinus totus: angulus a quantitas arcus cum qua intratur, in quamlibet dictarum trium tabellarum. 50 Et si ponatur ab gnomon, erit bc umbra versa, ad altitudinem anguli a. Et linea ac radius coniungens extrema gnomonis et umbrae.

Igitur intranti in tabellam sinus cum angulo a offertur sinus rectus, qui est linea bd nam da est sinus secundus ipsius anguli. Intranti autem in tabellam fecundam cum angulo a offertur umbra versa, qua est linea bc. Intranti demum tabulam beneficam cum angulo ipso a offertur linea ac quam radium appello.

51 Hinc patet structura et collatio harum trium tabellarum. Namque ex notitia duarum linearum, scilicet ab quae est sinus totus, et ex bd notescunt coeterae. In tabella itaque sinus recti, quando angulus a nihil est: sinus quoque bd nullus est: quando autem angulus a continet 30 gradus; sinus bd est dimidium ipsius ab sinus totius, quare scilicet est dimidium lateris hexagoni: quando vero angulus a habet 90 gradus, tunc bd est ipsa ab sinus totus.

52 In tabella vero foecunda, quando angulus a nihil est, umbra versa bc nulla est. Quando vero angulus a habet 45 gradus: umbra bc aequalis est ipsi ab gnomoni. Quando vero angulus a habet 90 gradus; umbra bc infinita est.

[A:12v]

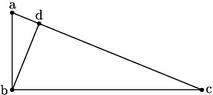
In tabella demum benefica, quando angulus a nullus est, tunc radius ac est par ipsi gnomoni ab. Quando autem angulus a habet 60 gradus: tunc radius ac est duplus ad gnomonem ab. 53 Quando vero angulus a 90 gradus complectitur: tunc radius ac infinitus est, sicut umbra bc aequidistant enim et in infinitum currunt absque concursu. Sed operae precium est intelligere, quo pacto ex his tabellis foecunda et benefica nonnullae quaestiones circa sphaeralia triangula resolvantur. Quam ob rem, superiori descriptione repetita.

Si in triangulo sphaerali agh detur angulus a et arcus gh, aio quod dabitur arcus ah, et coetera. 54 Nam, sicut in Sphaericis nostris demonstravimus sicut est quadratum gnomonis ad rectangulum ex umbris versis arcuum gh, ce, sic est sinus totus ad sinum arcus ah. Sed horum quatuor tria data sunt, scilicet quadratum gnomonis ac rectangulum ex umbris versis arcuum gh, ce datur, quoniam datur arcus gh et arcus ce, qui complementum est arcus eb dati propter angulum a datum. Et sinus totus datur. Igitur quartum, scilicet sinus arcus ah et ipse arcus ah dabitur. Hinc autem trahitur regula calculandi rectam ascensionem, ac regula supputandi differentiam ascensionalem, quibus utitur Ioannes Regiomontius. 55 Haec quo ad tabulam foecundam, in qua supposito gnomone ab particularum 100000, exarantur umbrae versae per singulos quadrantis gradus.

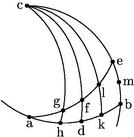
Veniam nunc ad nostram Beneficam. Sintque in triangulo sphaerali agh arcus ag, gh singuli dati. Aio quod dabitur arcus ah. Vocabo autem radium ac in tabula benefica inventum, numerum multiplicandum. 56 Itaque, quoniam, sicut in Sphaericis ostendimus, sicut est sinus totus ad numerum multiplicandum arcus gh²⁹ sic [A:13r] sinus arcus ge ad sinum arcus hb. Et horum tria data sunt. Igitur et quartum, scilicet sinus arcus hb et ipse arcus hb et eius complementum arcus ah dabitur³⁰.

Item in eodem triangulo agh dati sint arcus gh cum angulo a. Dico quod arcus ag et reliqui dabuntur.

57 Cum enim, sicut in Sphaericis ostendimus, sicut est sinus totus ad numerum multiplicandum arcus ce, iam dati propter angulum a et arcum eb datum: sic sit sinus arcus gh ad sinum arcus ag atque horum tria data sint; dabitur quartum scilicet sinus arcus ag et ipse arcus ag. Sicut proponitur. Item in ipso triangulo agh dentur arcus ag, gh dico quod dabitur angulus a et coetera.

58 Cum enim, sicut ostendimus in Sphaericis, sicut est sinus totus ad numerum multiplicandum arcus ge dati, propter arcum ag datum: sic sit sinus arcus gh dati ad sinum arcus eb. Quorum tria data sunt; dabitur quartum scilicet sinus arcus eb et ipse arcus eb, qui est quantitas anguli a. Quod est propositum.

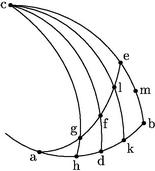
Quae data, quamquam per tabellam sinus sicut alia sexcenta, expediuntur, tamen eorum, per has tabellas foecundam et beneficam facilior succedit operatio. 59 Per has enim excluditur difficultas ac fastidium divisionis: quippe quae fit hic abiectis tantummodo figuris aliquid. Quot videlicet zifrae adhaerent monadicae figurae in numero repraesentante sinum totum, sive gnomonem, eiusve quadratum. Neque enim alia necessitas induxit Regiomontanum fabricandi tabellam foecundam: quem nos imitati nostram beneficam adinvenimus, servato gnomone ipsius Ioannis. 60 Quorum omnium demonstrationem nos in secundo Sphaericorum nostrorum libello, calculumque in problematibus astronomicis satis explicuimus. Quidquid autem diximus de triangulo sphaerali agh orthogonio, id totum de triangulo afd deque triangulo alk omnique alio sphaerali triangulo [A:13v] rectangulo fieri potest. 61 Hinc enim derivantur data reliquorum triangulorum sphaeralium, omnesque circa sphaerales arcus quaestiones, et regulae omnes, quibus Ptolemaeus utitur in sua Magna constructione, a Menelao sive Mileo geometra sumptis: unde tabula magna primi mobilis, et generales ac particulares declinationum et rectarum ascensionum tabulae ab egregio viro Ioanne Regiomontano supputatae sunt.