[A:8r] 14.^a

Trianguli circulum circumscribentis, si¹² data latera¹³ fuerint: datur circuli diameter.

Si enim triangulum fuerit orthogonium: excessus, quo aggregatum laterum rectum angulum continentium, excedit latus reliquum, est circuli quaesiti diameter. Quod inventum nonnulli tribuunt Archytae, quod nos in speculationibus nostris ostendimus. 18 Sed cum circulus intra triangulum descriptus tangat tria latera: et tres semidiametri ad puncta contactuum sint ad latera perpendiculares: planumque sit propterea, ex ductu talis perpendicularis in dimidium aggregati trium laterum, produci aream trianguli: iam ob id, area trianguli per alteram praemissarum data¹⁴ in dimidium aggregati laterum divisa eliciet quaesitam circuli semidiametrum. In omni triangulo.

15.^a

19 Data circuli diametro, dabuntur latera decagoni, hexagoni, pentagoni, quadrati, atque trianguli isopleurorum eidem circulo inscriptorum.

Esto semicirculus abg super diametrum ag centrumque d; bd perpendicularis ad ag;// dg secetur per aequalia in puncto e // ductaque eb; ipsa eb aequalis sit ez et connectatur bz et ab. Item ipsa ab perpendicularis: ipsique bd aequalis sit bh et coniungatur ah. // 20 Erit enim dz latus decagoni, bd latus hexagoni, bz latus pentagoni, ab latus quadrati, ah latus trianguli aequilaterorum tali circulo inscriptorum.// Sicut in 13^o Elementorum Euclidis, et Ptolemaeus in principio Magnae Constructionis ostendit.

[A:8v]

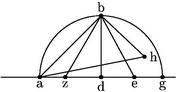
16.^a

Dato alicuius praedictarum figurarum latere, dabitur circuli intra quem figura describitur, diameter.

21 Detur, exempli causa, latus decagoni a aio quod dabitur, circuli intra quem decagonus describitur, diameter. Exponatur quaecumque diameter circuli b, iam dabitur, per praecedentem, latus decagoni circulo, cuius diameter b inscripti: sit illud c; // per 7^am dabitur his quarta proportionalis, ut scilicet sicut c ad b sic sit a ad d. Eritque d¹⁵ diameter circuli intra quem describitur decagonum, cuius latus a proponitur propter proportionem figurarum.

Corollarium

22 Hinc autem per 9^am huius¹⁶, dabitur perpendicularis a centro ad latus quodlibet figurae aequilaterae intra circulum descriptae. Et ex¹⁷ ductu perpendicularis in dimidium perimetri figurae, consurgit ipsius figurae area. Quae problemata facile convertuntur, sicut in hac 16^a factum est.

17.^a

Data alicuius arcus chorda, datur chorda residui de semicirculo.

Nam cum tales chordae cum diametro semicirculi contineant angulum rectum: absolvetur propositio per 9^am huius.

18.^a

23 Datis chordis inaequalium arcuum in semicirculo, dabitur chorda arcus excessus.

Dabitur enim ex praemissa¹⁸ per primam huius, rectangulum ex chorda maiore, in chordam residui de semicirculo arcus minoris; sed tale rectangulum ut ostendit Ptolemaeus¹⁹ aequale est duobus, scilicet rectangulo ex chorda minore in chordam residui de semicirculo arcus maioris quod datur per praemissam et primam²⁰: atque rectangulum ex semidiametro in chordam arcus excessus. 24 Igitur hoc tertium rectangulum datur, sed semidiameter data, [A:9r] igitur per 2^am huius, chorda arcus excessus datur.

19.^a

Data chorda cuiusvis arcus; dabitur chorda dimidii talis arcus.

Dabitur enim, per antepraemissam, chorda residui de semicirculo: huius quoque chordae ac diametri dabitur differentia: et huius differentiae dimidium. 25 Sed chorda dimidii propositi arcus media proportionalis est inter dictae differentiae dimidium ac diametrum: ut ostendit Ptolemaeus. Dantur autem dictum dimidium ac diameter: ergo, per sextam huius, dabitur chorda dimidii propositi arcus: quae media est trium continue proportionalium.

20.^a

Datis duorum arcuum chordis: dabitur chorda arcus ex his compositi.

26 Nam, per 17^am huius, dantur chordae residuorum de semicirculo: dabuntur ergo duo rectangula, quae ex utraque datarum chordarum in chordam residui de semicirculo alterius fiunt, quae²¹ pariter sumpta aequalia sunt rectangulo, quod ex diametro²² in chordam arcus ex arcubus propositis compositi producitur ut ostendit Ptolemaeus²³. Datur ergo tale rectangulum. Sed diameter data: ergo et chorda arcus dicti ex arcubus datis compositi datur per secundam huius.

Scholium

27 Ex his sex praeceptis a Ptolemaeo traditis emanat omnis chordarum ac sinuum rectorum calculatio. Nam²⁴ nunc dividendo, nunc componendo arcus, notescunt chordae ac sinus non solum singulorum arcuum, sed etiam per singulos graduum quadrantes, immo si lubet per singulas minutias: completa autem tabula chordarum per totum semicirculum, aut sinuum per totum quadrantem, parata est via triangulorum tam planorum, quam sphaeralium calculo. 28 Namque [A:9v] quantitates angulorum per proportionem laterum, et ergo per sinus rectos cognoscuntur: et arcus circulorum in sphaera per sinus similiter notescunt: sicut in Sphaericorum libris traditur. Sed nos hic pro triangulis adducemus exemplum.