9.^a

10 In triangulo rectangulo, si dentur duo latera, datur reliquum.

Nam cum per penultimam Primi Elementorum quadrati laterum rectum angulum comprehendentium simul sumpta sint aequalia quadrato reliqui lateris: ex 3^a huius absolvitur propositum.

10.^a

11 Trianguli, cuius data sunt latera, datur quilibet kathetus.

Trianguli abc data sint latera singula. Aio quod dabitur a quovis⁶ angulo ad oppositum latus perpendicularis: utpote cd. // Nam si latera ac, cb sint aequalia, palam est, quod cd cadit in punctum medium inter ab. 12 // Itaque in triangulo rectangulo bcd, cum duo latera⁷ db, bc dentur: dabitur per praemissam cd reliquum, kathetus scilicet quaesitam.

Si vero ac, cb latera sint inaequalia: tunc iam per penultimam Primi Elementorum differentia quadratorum ac, cb iam data, est differentia quadratorum ad, db iam data. 13 Sed talis differentia, per 6^am 2ⁱ⁸, divisa per ipsam ab exhibet differentiam ipsarum ad, db.

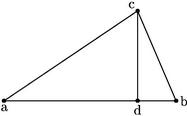
[A:7v] Cum ergo ipsarum ad, db detur aggregatum per hypothesim et nunc differentia: dabuntur ad, db singulae. Nam dimidium differentiae adiectum et subtractum dimidio dicti aggregati, conflabit et residuabit ipsas ad, db singulas. Unde⁹ rursum kathetus dabitur.

11.^a

14 Trianguli, cuius dantur latera: datur area.

Dabitur enim per praecedentem kathetus ab angulo ad basim: quod autem ex dimidio basis in kathetum producitur, est area trianguli per 42^am Primi Elementorum. Igitur per primam huius, talis area datur.

12.^a

Trianguli, cuius datur basis, et kathetus ad basim datur area.

15 Nam ex 1/2 basi in kathetum¹⁰. // Si data sit basis et area, dabitur kathetus. Nam¹¹ divisa area in dimidium basis, exit ex divisione kathetus. Denique, si detur kathetus et area, datur basis: nam area in kathetum divisa, prosilit ex divisione dimidium basis.

Corollarium

Ex quibus manifestum est, quod cum in orthogonio triangulo latera rectum angulum comprehendentia sint pro kathetis, iam ex dimidio utriuslibet talium laterum in reliquum producitur area trianguli ipsius. 16 Et ex divisione areae in dimidium utriuslibet dictorum laterum, exultat latus reliquum.

13.^a

Trianguli, cuius dantur latera, absque notitia katheti, datur area.

Datur enim aggregatum laterum. Datur eius dimidium. Dantur tres excessus, quibus id dimidium excedit singula latera. Datur et solidum sub tribus excessibus comprehensum. 17 Dabitur et per 6^am huius, media proportionalis inter dictum dimidium solidumque magnitudo, quae, ut alibi nos ostendimus, est area trianguli.