[S:152] [C:1v]

APOLLONII PERGAEI CONICORUM ELEMENTORUM

LIBER QUINTUS

I.

Duarum sectionum conicarum eiusdem nominis, eumdem axim, eamdem diametrum, eumdemque verticem habentium: illa, quae maiorem sortitur rectam diametrum, in ipso vertice tangit reliquam, exterius incedens et alibi non coincidens.

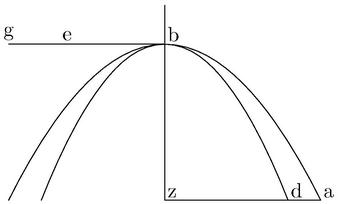
Ut si parabola ab, cuius recta bg atque parabola db, cuius recta be, minor quam bg, ambae circa axem bz, verticemque b consistant. Aio quod sectio ab ipsam db continget, apud punctum b tantum et semper extra ipsam db ibit. Capiatur enim in axe utcunque relictum z punctum²⁰ et ordinate ducatur zda, secans apud²¹ d, a puncta peripherias. Et tunc per 11. 1. Conicorum az poterit rectangulum gbz, nec non dz poterit rectangulum²² ebz. Maius autem rectangulum²³ gbz, quam rectangulum²⁴ ebz, quandoquidem bg²⁵ supponitur maior quam be. Igitur az²⁶ longior quam dz et perinde punctum a²⁷ est extra peripheriam sectionis db. Similiter ostendam quod omnia puncta periphaeriae ab atque ideo tota ipsa ab peripheria cadit utrinque extra sectionem DB²⁸, in solo b puncto ipsam tangens. Quod fuit demonstrandum. Item sit hyperbole ab, cuius transversa diameter bg, recta vero bd, et hyperbole²⁹ eb, cuius transversa bg, recta bz brevior quam bd, ambae sub eodem vertice b et super eundem axim³⁰ gbh constitutae. Aio iam quod sectio ab tota extra sectionem eb cadit, ipsam in solo b puncto³¹ contingens. Capiatur enim in axe ubivis relictum punctum h, per quod ordinate ad axim agatur linea hea, secans sectionum peripherias³² apud e, a, ipsisque gd, gz coniunctis, productisque, occurrens apud k, t puncta.

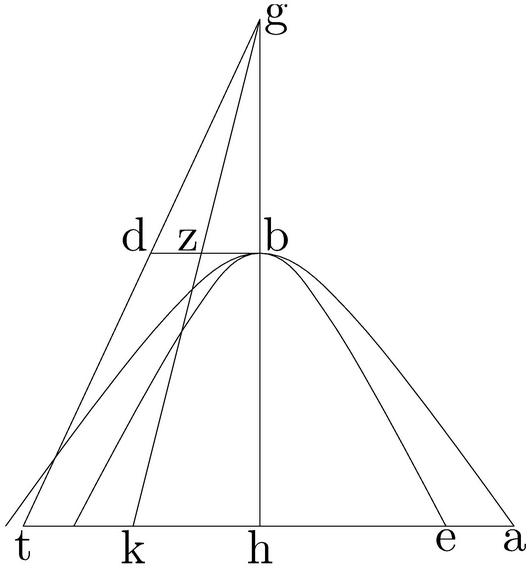
Et tunc per 12. primi Conicorum Elementorum, ah poterit rectangulum bht, item eh poterit rectangulum³³ bhk. Maius³⁴ autem rectangulum bht, quam rectangulum bhk, quia³⁵ db³⁶ supponitur maior quam bz. Igitur ah longior [C:2r] quam he et ideo punctum a extra sectionem eb. Similiter ostendam quod omnia puncta peripheriae ab, ipsaque peripheria tota cadet utrinque extra sectionem eb, in solo puncto b ipsam tangens. Quod fuit demonstrandum.

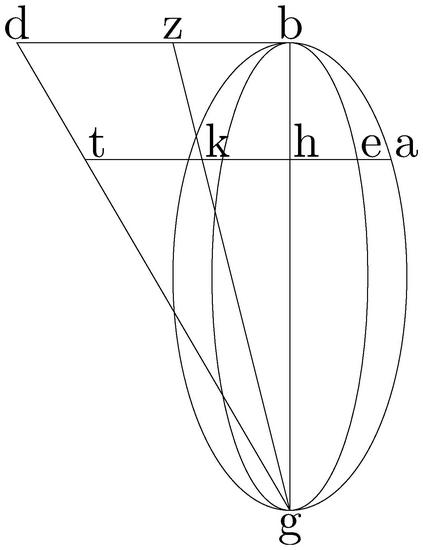
Demum sit Ellipsis ab, cuius transversa bg, recta vero bd, et ellipsis eb, super eamdem diametrum bg, habens rectam bz breviorem ipsa bd. Aio iam quod sectio bag tota extra sectionem beg cadet, solumque ipsam in ipsis b, g verticibus tanget. Capiatur enim in axe bg punctum ubicunque h, per quod ordinate ducta, peripheriis apud a, e, ipsisque gd, gz, coniunctis apud³⁷ t, k³⁸ puncta coincidat. Et tunc per 13. primi Conicorum, ah poterit rectangulum bht, item eh poterit rectangulum bhk. Unde, ut supra factum est, arguetur ah longior quam he. Et perinde peripheria bag, extra peripheriam beg, exceptis punctis b, g, in quibus sese contingunt. Quemadmodum proponitur demonstrandum.[S:153]

SCHOLIUM.

Quod si ellipsis ab, ellipsim eb, transversa tantum, vel non solum recta diameter³⁹, sed etiam transversa superaret, non minus sequeretur id, quod demonstratum est fieretque contactus in solo vertice b. Item pro puncto z, sive h, quod in axe assumitur, posset assumi ad libitum punctum a, sive d, aut e in utravis peripheria, ad demonstrandum quod altera peripheria extra alteram incedit.

COROLLARIUM.

Unde manifestum est, quod proposita parabola⁴⁰ possunt circa eius axem verticemque, tam extra quam intus, infinitae parabolae describi, quae propositam seseque invicem in ipso dumtaxat vertice contingant. Atque idem de hyperbolis, ellipsibus, circulisque dicendum.