PRAEAMBULUM

110 Verum in multiplicationibus binomiorum ac residuorum hoc est praenotandum, quod si nomina multiplicanda inscribantur per plus aut per minus utraque, tunc productum ex eorum multiplicatione factum inscribendum erit per plus; si vero alterum nominum per plus, alterum per minus notetur, productum per minus notandum erit. Quod ita esse brevi demonstratione arguemus. 111 Sunto duo residua, unum ab bc, alterum de ef, cum enim residua ipsa sint quantitates ac df quae restant per abscisionem¹¹³ minorum nominum a maioribus, illud sic pronuntiatur ab minus bc hoc est, quod superest, subtracta quantitate bc a quantitate ab; aliter enim exprimi non potest, cum sit quantitas irrationalis, per abscisionem¹¹⁴ quantitatis a quantitate sibi incommensurabili factam, relicta. 112 Et similiter alterum sic profertur de minus ef¹¹⁵ hoc est, quod [C:102v] relinquitur, dempta quantitate ef a quantitate de; illud inquam residuum est quantitas ac sicut dictum est, relicta. Hoc autem residuum, quantitas df per similem abscisionem¹¹⁶ remanens. Quae cum aliter quam per nominum ex quorum abscisione¹¹⁷ generantur, hoc est, quorum excessus sunt, proferri nequeant; iam si alterum in alterum multiplicandum erit, talis multiplicatio non nisi per nominum multiplicationem fieri poterit. 113 Si igitur residuum ab¹¹⁸ bc multiplicandum est in¹¹⁹ residuum de ef, non aliter multiplicatio fieri potest, quam multiplicando haec nomina singula in illa singula. Unde fiet quadruplex multiplicatio: prima scilicet ab in [S:103] de; secunda ab in ef; tertia de in bc; quarta bc in ef. Harum prima, per primam secundi Elementorum Euclidis, continet quatuor multiplicationes se ipsam integrantes, scilicet ac in df; ac in ef; bc in df; bc in ef. 114 Secunda continet duas multiplicationes se ipsam perficientes, scilicet ac in ef; et bc in ef. Tertia item duas, ex quibus componitur, scilicet bc in df; bc in ef. Quoniam scilicet producta partium integrant productum integrorum. Quarta vero unica est, scilicet bc in ef, quoniam fit ex nominibus indivisis; [C:103r] et cum praedictis octo posita facit novem multiplicationes. 115 Productum autem quaesitum est, quod fit ex multiplicatione ac in df, quod haberi non potest nisi peractis dictis quatuor multiplicationibus, quae continent novem ductus; ex quibus cum sumendum¹²⁰ sit solum illud quod fit ex ac in df, necesse est caetera octo producta esse abiicienda, quod fieri non potest nisi dimidium eorum notetur per plus ac reliquum dimidium per minus, atque ita alterum altero repensante, summa quaesita, quae fit ex ac in df servetur intacta. 116 Sed ex dictis¹²¹ caeteris octo productis tria primae¹²² multiplicationis scilicet quae fiunt ex ac in ef, ex bc in df, et ex bc¹²³ in ef inscribi debent per adverbium plus¹²⁴, quoniam sunt membra primae multiplicationis, quae fit ex nominibus ab de per idem adverbium notatis. 117 Duo autem producta secundae multiplicationis ex ac in ef et bc in ef notanda per adverbium minus, quoniam sunt membra secundae multiplicationis¹²⁵, quae fit ex nominibus ab ef quorum alterum per adverbium minus inscribitur. Duo quoque producta tertiae multiplicationis ex¹²⁶ bc in df et ex bc in ef similiter per adverbium minus notata intelliguntur, quoniam tertia multiplicatio, cuius¹²⁷ membra sunt, constat ex nominibus de bc quorum alterum per minus notatur. [C:103v] 118 Octavum igitur productum, quod fit ex bc in ef nominibus inscriptis per minus, necesse est, ut inscribatur per plus; atque ita fiant quatuor producta inscripta¹²⁸ per plus, et totidem producta paria inscripta per minus; et perinde tantum his minuentibus, quantum illa superaddunt, summa quaesita, quae fit ex ac in df, intacta permaneat. Constat igitur, quod ex ductu nominum per adverbium minus notatorum producitur quantitas per adverbium plus notanda. 119 Sed illud exemplum satis esse debet, quod plus in plus multiplicatum, sive minus in minus, omnino producit plus; quemadmodum affirmatio affirmationis affirmat; et negatio negationis affirmat similiter. Item sicut affirmatio negationis, sive negatio affirmationis negat; ita [S:104] sive plus in minus, sive minus in plus multiplicatum producit minus. Potes exemplificare regulam et comprobare demonstrationem per numeros rationales, ut sic singulae novem multiplicationes distinctae appareant, et facilius omnia intelligantur.

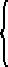ac df + ab 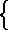ac ef plus + de bc df plus +   bc df -

ah 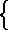ac ef minus + ef bc ef minus -

de 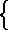be de minus + bc bc ef minus -

bc bc ef plus - ef