PROPOSITIO XXXVI.

Sphaera aequalis est pyramidi, cuius basis aequalis est sphaericae superficiei, celsitudo autem sphaerae semidiametro.

Esto sphaera A, pyramis autem P, basim habeat aequalem superficiei sphaerae A; celsitudinem vero aequalem semidiametro sphaerae A. Aio quod aequalis est P pyramis sphaerae A. Sit enim conus M basim habens aequalem superficiei sphaerae A, celsitu[S:83]dinem vero aequalem semidiametro sphaerae A: itaque P pyramis, et M conus, et bases, et celsitudines invicem aequales habent.

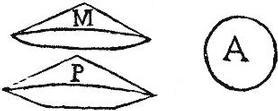
Quare per 2. corollarium 33. em praecedentis. aequalis est P pyramis cono M: sed conus M per 24. aequalis est sphaerae A: ergo et P pyramis aequalis est sphaerae A: quod est propositum.

COROLLARIUM I.

Unde manifestum est quod prisma, cuius basis aequalis est superficiei sphaerae, celsitudo autem aequalis semidiametro sphaerae, est triplum ad sphaeram: quoniam per 8.12. tale prisma triplum est suae pyramidis, quae aequalis est sphaerae.

COROLLARIUM II

Quare prisma, cuius basis aequalis est superficiei sphaerae, celsitudo vero tertia pars semidiametri sphaerae est aequale ipsi sphaerae.

COROLLARIUM III.

Et quoniam superficies sphaerae per 10. huius, aequalis est rectangulo, quod fit ex diametro sphaerae in peripheriam sui maximi circuli: ideo sphaera aequalis est ei solido parallelepipedo, cuius basis est dictum rectangulum, celsitudo autem tertia pars semidiametri sphaerae.

COROLLARIUM IV.

Manifestum est ergo, quod ex ductu semidiametri sphaerae in superficiem eius producitur triplum soliditatis sphaerae: nam tale productum est soliditas prismatis habentis basim aequalem superficiei sphaerae, et altitudinem aequalem semidiametro sphaerae.

COROLLARIUM V.

Quamobrem ex ductu tertiae partis semidiametri in superficiem sphaerae producitur soliditas sphaerae.