PROPOSITIO XXXV.
Pyramidis, et coni ratio componitur ex basium et celsitudinum rationibus.
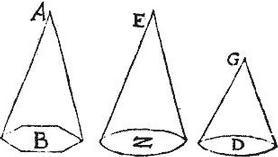
Sit pyramis AB, cuius basis B, et celsitudo AB: item conus GD, cuius basis D, et celsitudo GD. Aio quod ratio pyramidis AB ad conum GD componitur ex ratione basis B ad basim D, et ex ratione altitudinis AB ad altitudinem GD. Ponatur enim conus EZ super circulum Z aequalem circulo D: vel pyramis EZ super basim Z aequalem basi D, cuius altitudo EZ sit aequalis altitudini AB, eritque per 33. praemissam, pyramis AB ad conum EZ, vel per 8.12. ad pyramidem EZ, sicut basis B ad basim Z, et per 11.12. Si EZ sit conus (vel per praemissam si sit pyramis,) erit conus EZ, vel pyramis EZ ad conum GD, sicut celsitudo EZ ad celsitudinem GD: verum ratio pyramidis AB ad conum GD componitur ex ratione pyramidis AB ad conum, sive pyramidem EZ, et ex ratione coni, sive pyramidis EZ ad conum GD: ergo eadem ratio pyramidis AB ad conum GD componetur ex ratione basis B ad basim Z, vel basim D (cum sint aequales) et ex ratione celsitudinis EZ vel celsitudinis AB, cum sint aequales, ad celsitudinem GD: et hoc erat demonstrandum.
COROLLARIUM I.
Manifestum est ergo quod similiter prismatis, et cylindri ratio ex basium, et celsitudinum rationibus componitur: cum prisma pyramidis, et cylindrus coni sit triplus.
COROLLARIUM II.
Unde facillime sequitur, ut pyramis, et conus, quorum bases sunt fastigiis reciprocae sint invicem aequales: contra si pyramis, et conus ad invicem extiterint aequales, eorum bases erunt fastigiis reciprocae; et hoc idem de prismate, et cylindro sentiendum.