PROPOSITIO XXVIII.

Cylindrus, cuius tam axis, quam basis diameter aequalis est sphaerae, diametro sesquialter est ad sphaeram.

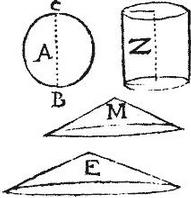
Quamvis haec propositio demonstrata sit in praemissa 26. ut ipsius corollarium, placuit tamen hic eam aliter demonstrare. Esto sphaera quidem A cylindrus Z, sitque tam axis Z cylindri, quam diameter aequalis sphaerae A diametro CB. Aio quod cylindrus Z sesquialter est ad sphaeram A. Sit enim conus M basim habens aequalem superficiei sphaerae A, et celsitudinem aequalem semidiametro sphaerae AB: eritque per 25. praemissam conus M aequalis sphaerae A: item sit conus E basim habens aequalem universae superficiei cylindri Z, et celsitudinem aequalem semidiametro basis cylindri: eritque per praecedentem. conus E aequalis cylindro Z (cum semidiameter sphaerae A, et cylindricae basis, quae sunt celsitudines conorum M, E, sint aequales per hypothesim;) atque cylindri Z tota superficies, quae basis est coni E, sesquialtera sit, per corollarium 11. superficiei sphaerae A, quae basis est coni M: et coni eiusdem altitudinis per 11,12. sint ad invicem sicut bases: iam et conus E sesquialter erit ad conum M: verum conus M sphaerae A, conusque E cylindro Z fuit aequalis: ergo et cylindrus Z sesquialter erit ad sphaeram A: quod fuit propositum.

COROLLARIUM.

Rursum ergo hinc patet, quod sphaera dupla est ad conum, cuius tam axis, quam basis diameter aequalis est sphaericae diametro: nam cum cylindrus huiusmodi sit per praemissam ad sphaeram sesquialter ad conum vero, per 9.12. triplus, erit sphaera ad conum dupla. Itaque sphaera sic se habet ad cylindrum, et reliqua tornatilia: nunc ad segmentorum soliditates transibimus.