PROPOSITIO XXIX.
Si circuli arcus quispiam in portiones secetur aequales, quibus chordae subtendantur, et arcus extrema, cum centro circuli connectantur: rectilineum autem sub chordis, et semidiametris comprehensum, altera semidiametrorum stante, semel circumducatur: descriptum solidum aequum est ei cono, cuius basis aequalis est conicis superficiebus per chordas descriptis, celsitudo vero aequalis perpendiculari, quae a centro circuli ad quamlibet chordarum egreditur.
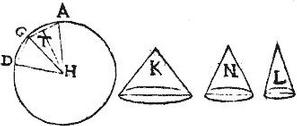
In circulo AD, cuius centrum H, arcus AD secetur in quotvis partes aequales, ut puta duas AG, GD, quibus subtendantur chordae AG, GD, et ductis semidiametris AH, DH circumducatur rectilineum AD stante semidiametro AH, ut describatur solidum AD. Sitque conus K, cuius basis sit aequalis conicis superficiebus descriptis per chordas AG, GD, celsitudo autem aequalis perpendiculari HT ad latus AG. Aio quod aequalis est conus K solido AD: connectatur enim GH, et constituantur sub celsitudine HT duo coni scilicet conus L basim habens aequam conicae superficiei, quam describit linea AG: et conus N basim habens aequam conicae superficiei, quam describit linea GD: unde conorum L, N, bases simul aequales erunt basi coni K, quae fuit dictis conicis superficiebus aequalis: quare per 21. huius, coni L, N, simul aequales erunt cono K: sed per 23. solidum a triangulo HAG descriptum aequum est cono L, quodque per triangulum GHD describitur aequum est cono N. Ergo solidum AD, quod a toto rectilineo AD, describitur, aequum est aggregato conorum L, N. Fuit autem hoc aggregatum cono K aequale: igitur et AD solidum cono K erit aequale: quod demonstrandum proponitur.
Hoc idem ostendemus quotcunque fuerint chordae factis tot conis quot fuerint triangula, qui singuli sunt singulis solidis per triangula descriptis aequales, adhibitis semper 21. et 23. huius, estque similis demonstratio 24. huius.