PROPOSITIO XXVII.
Si fuerit axis cylindri aequalis diametro basis, coni autem basis aequalis universae superficiei cylindri, celsitudo vero aequalis semidiametro cylindricae basis, aequalis erit cylindrus cono.
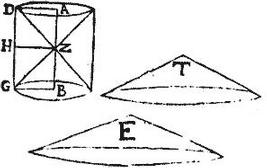
Rectanguli ABGD latus AB duplum sit lateris BG, et circumducto rectangulo semel manente latere AB, describatur cylindrus AG. Itaque cum BG, quae semidiameter est basis, sit dimidium axis AB erit tota diameter aequalis axi. Item sit conus E, cuius basis sit aequalis universae cylindri AG superficiei, hoc est aggregato ex curva superficie, quam describit linea GD, et ex basibus, quas describunt lineae AD, BG celsitudo vero semidiametro AD. Aio quod cylindrus AG, et conus E sunt aequales; secetur enim axis AB bifariam apud Z, et connectantur DZ, ZG quo fiet, ut in circumductu rectanguli AG ipsa triangula ZDA, ZGB describant conos, quorum bases, quae et cylindri, et quarum vertex punctum Z. Cadat autem perpendicularis a puncto Z ad DG, quae sit ZH, sitque conus T, cuius basis sit aequalis cylindricae superficiei, quam describit [S:73] linea GD, celsitudo vero aequalis perpendiculari ZH, et ideo semidiametro AD, quae celsitudo est coni E; eritque per tertiam partem 23. praecedentis, conus T aequalis solido descripto per triangulum DZG. Quamobrem conus T cum conis descriptis per triangula ZDA, ZGB, simul aequalis erit toti cylindro AG; basis quoque coni T cum basibus cylindri aequalis erit universae superficiei cylindri, et ideo basis coni T cum basibus conorum ADZ, BGZ, quae sunt bases cylindri, simul aequales erunt basi coni E, quae fuit aequalis universae superficiei cylindri; estque horum quatuor conorum celsitudo una, quoniam lineae AD, AZ, ZB, ZH, quae fuerunt conorum celsitudines sunt aequales. Igitur per 21. praedictam, conus E aequalis est aggregato conorum T, ADZ, BGZ; fuit autem hoc aggregatum aequale cylindro AG: ergo cylindrus AG aequalis erit cono E, quod est propositum.