PROPOSITIO XII.

Si circulo duae aequilaterae, et aequiangulae figurae una inscribatur, altera circumscribatur correspondentibus angulis, et diametro stante, tam semicirculus, quam figurarum dimidia, donec ad locum suum redeant, circumvolvantur; descriptae a semicirculo sphaerae superficies media proportionalis inter solidorum a dimidiis figurarum descriptorum superficies.

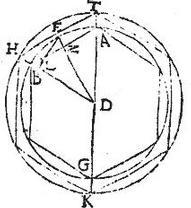
Circulo ABG, cuius diameter AG, centrumque D inscribatur figura aequilatera, cuius laterum unum sit AB, et secto arcu AB bifariam in signo E, et ducta semidiametro DE secante chordam AB in puncto Z bifariam, et orthogonaliter ducatur HET ad rectos ipsi DE: et ideo contingens circulum in puncto E per 15.3. quae ipsis DA, DB semidiametris productis occurrat ad signa H, T, eritque TH latus figurae aequilaterae, et aequiangulae circumscribentis circulum ABG, et similis ipsi figurae ABG inscriptae. Compleatur itaque figura circumscripta, sitque THK, et circumducatur semel tam semicirculus ABG, quam semipolygonium ABG quamque semipolygonium THK super axem TK stantem. Aio itaque quod superficies sphaerae, quam describit semicirculus ABG media proportionalis, est inter superficiem solidi, quod describit semipolygonium ABG, et inter superficiem solidi, quod describit semipolygonium THK, quod sic ostendo. Cadat a signo E ad DB perpendicularis EL, eruntque triangula DEL, DBZ invicem aequilatera; quare ipsae DZ, DL aequales per corollarium autem 3. nonae huius, ex DZ, et ideo ex DL in peripheriam ABG fit dimidium superficiei solidi descripti a semipolygonio ABG per 10. autem huius, ex DB semidiametro in peripheriam circuli ABG fit dimidium superficiei sphaerae descriptae a semicirculo ABG. Adhuc per corollarium 3. nonae. ex DE in peripheriam circuli THK circumscribentis polygonum, et ideo ex DH in peripheriam circuli ABG: (sunt enim haec duo aequalia per secundum corollarium 6. huius.) fit dimidium superficiei descriptae a semipolygonio THK. Igitur haec tria producta, quae sunt dimidia dictarum superficierum, sunt per 1. sexti ad invicem sicut lineae DL, DE, DH, quae sunt bases productorum, nam altitudo est aequalis periphaeriae circuli ABG: sed DL, DE, DH sunt continuae proportionales, propter similitudinem triangulorum DEL, DHE: ergo tria producta, quae sunt dimidia dictarum superficierum sunt continue proportionalia. Quare et earum dupla, totae scilicet superficies sunt continuae proportionales: itaque superficies solidi descripti a semipolygonio ABG, superficies sphaerae descriptae a semicirculo ABG, superficies solidi descripti a semipolygonio THK sunt continuae proportionales in proportione scilicet ipsarum DL, DE, DH, linearum: quod est propositum. [S:55]

SCHOLIUM.

Quod si aequilaterae, et aequiangulae figurae rectilineae duo circuli unus circumscribatur, aliter inscribatur, et diametro manente tam semipolygonium, quam duo semicirculi circumducantur, descripti quoque a semipolygonio solidi superficies media proportionalis est inter sphaerarum a semicirculis descriptarum superficies. Descriptioni praecedentis addatur circulus THK circumscriptus figurae rectilineae THK, et sphaera per revolutionem semicirculi THK descripta. Aio iam quod solidi THK superficies media proportionalis est inter sphaerarum ABG, THK superficies. Nam per 10. ex recta HD, in peripheriam circuli THK fit dimidium superficiei sphaerae THK, atque, ut in praemissa, ostensum est, ex recta HD in peripheriam circuli ABG fit dimidium superficiei solidi THK. Quare per primam sexti superficies sphaerae THK ad superficiem solidi THK erit sicut peripheria circuli THK ad peripheriam circuli ABG et ideo per sextam sicut semidiameter DH ad semidiametrum DE: sed fuit in praemissa, sicut DH ad ipsam DE; sic superficies solidi THK ad superficiem sphaerae ABG: ergo et sicut superficies solidi THK ad superficiem sphaerae ABG sic superficies sphaerae THK ad superficiem solidi THK. Itaque superficies solidi THK media proportionalis est inter sphaerarum THK, ABG superficies; quod erat demonstrandum.

COROLLARIUM.

Manifestum est ergo quod si circulo polygonium aequilaterum, et polygonio rursum circulus; et circulo adhuc polygonium respondentibus angulis: et ita deinceps, quoties lubet, inscribatur, et diametro manente tam semicirculi, quam semipolygonia circumducantur; descriptarum sphaerarum, et tornatilium solidorum superficies sunt continuae proportionales secundum inscriptionis ordinem. Hactenus de solidi tornatilis, ac sphaerae superficie, nunc de segmentorum a dictis solidis abscissorum superficiebus verba faciemus.