PROPOSITIO XI.

Sphaerae superficies quadrupla est ad suum maximum circulum, estque aequalis curvae superficiei eius cylindri, cuius tam axis, quam basis diameter aequalis est sphaerae diametro.

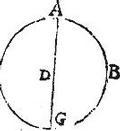
Esto sphaera ABG, quam describat semicirculus ABG, stante diametro AG circumductus, cuius centrum D. Aio quod superficies sphaerae ABG quadrupla est ad circulum ABG. Nam per praemissam. Sphaerae ABG superficies aequalis est ei, quod fit ex diametro AG in peripheriam circuli ABG: per 4. vero libelli de dimensione circuli, area circuli aequalis est ei, quod fit ex semidiametro DG in dimidium periphaeriae totius circuli ABG: estque per 18. sexti quod fit ex diametro AG in peripheriam circuli, ABG quadruplum ad id, quod ex semidiametro DG in peripheriam semicirculi ABG (quandoquidem latera singulorum laterum dupla.)

Igitur sphaerae ABG superficies quadrupla est ad circulum ABG maximum in sphaera: quod est primum ex propositis. Reliquum sic ostendo. Sit cylindrus, cuius tam axis, quam basis diameter sit aequalis diametro AG: aio quod sphaerae ABG superficies aequalis est curvae superficiei huiusmodi cylindri: nam talis cylindri basis erit circulus ABG, quare per 4. huius curva superficies ipsius cylindri aequalis erit ei, quod ex diametro AG in peripheriam circuli ABG: sed hoc aequale est sphaericae superficiei. Ergo sphaerica superficies aequalis erit curvae superficiei talis cylindri; quod supererat demonstrandum.

COROLLARIUM.

Manifestum est ergo quod cylindri, cuius tam axis, quam basis diameter aequalis est sphaerae diametro, tota superficies est ad sphaerae superficiem sesqui a la[S:54]tera: namque duae bases, cylindri sunt dimidium sphaericae superficiei, et cum sphaerica superficies sit quadrupla ad unam illarum, et curva superficies cylindri aequalis sphaericae superficiei: igitur tota cylindri superficies, quae constat ex curva superficie, et basibus continet sphaericam superficiem, semel, et insuper eius dimidium.