PROPOSITIO XIII.

Conicae superficies segmenti, quod sumitur a vertice solidi descripti a semipolygonio aequilatero ad unum circulorum ab angulis descriptorum, coniunctae sunt aequales ei, quod fit ex ductu lateris circumductae in peripherias descriptas ab angulis minus dimidio periphaeriae circuli segmentum solido abscindentis.

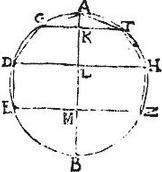
Intra circulum AB cuius diameter AB describatur polygonium aequalium laterum AGB, cuius dimidio semel circa diametrum AB stantem circumducto describatur solidum tornatile, de quo sumatur segmentum a vertice A ad unum circulorum ab angulis descriptorum, ut puta ad circulum descriptum ab angulo E, quod sit segmentum AEZ. Aio quod conicae superficies segmenti AEZ, quae scilicet a lateribus AG, GD. DE describuntur, aequales sunt simul ei, quod fit ex latere AG in aggregatum ex peripheriis ab angulis G, D, E minus dimidio [S:56] peripheriae descriptae ab angulo E. Ducantur enim GT, DH, EZ, secantes diametrum AB apud K, L, N, secabunt autem ad angulos rectos: itaque per 2. huius conica superficies, quam describit linea AG aequalis est ei, quod ex AG in dimidium peripheriae quam describit punctum G.

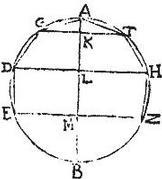
Item per 7. conica superficies coni-coluri, quam describit linea GD aequalis est ei, quod ex GD in dimidias peripherias descriptas a punctis G, D, item per 7. conica superficies, quam describit linea DE, sive per 4. si LDEM sit parallelogrammum, ac ideo superficies descripta cylindrica aequalis est ei, quod ex DE, vel AG in dimidias peripherias descriptas a punctis D, E. Huc ergo concurrunt integrae peripheriae descriptae a punctis G, D, et dimidium eius, quae describitur a puncto ultimo E. Quare per primam 2. Elementorum. omnes conicae superficies descriptae a lineis AG, GD, DE, quae est superficies segmenti AEZ, aequalis est ei, quod fit ex ductu lateris AG in omnes peripherias descriptas ab angulis G, D, E minus dimidio periphaeriae descriptae ab angulo E infimo, quae peripheria est circuli abscindentis segmentum AEZ de toto solido per semipolygonium descripto, quod erat demonstrandum. Hoc idem ostenditur etiam si chorda AG non fuerit latus polygonii aequilateri circulo inscripti, dum arcus AG, GD, DE sint aequales.