PROPOSITIO VIII.
Sit rursum libra AG, cuius medium B, trigonum autem DGH amblygonium, habens angulum, qui ad H obtusum; et latus DH perpendiculare ad AG. Et productum occurrat ipsi AG ad signum B, ut scilicet GB altitudo trigoni sit librae dimidium; et suspendatur a signis B, G, spatium autem Z suspensum a signo A aequae repat cum trigono HDG, sic se habente, ut nunc iacet: aio quod triplum est trigonum HDG spatii Z; apponatur enim spatio Z, spatium L, quod sit trigoni BGH pars tertia, et aeque repet per conversam praemissae, spatium L trigono BHG, sed ipsum Z [S:184] spatium aeque repit per hypothesim trigono DGH: ergo et totum ZL spatium aeque repet trigono BDG toti: quando centra gravitatum triangulorum BGH, HDG sunt in una recta, quae penes BD, atque ideo ab uno signo, in quo praedicta recta occurrit ipsi BG, appensa iacent ut nunc sunt: quamobrem per praecedentem, triplum est triangulum BDG totum spatii ZL totius; sed trigonum BHG triplum spatii L, ablatum ablati: ergo et HDG triplum spatii Z relictum relicti: quod est propositum.
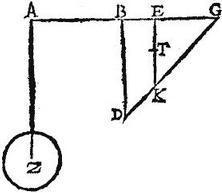
Demonstratur et haec propositio aliter, secetur GH apud E, ut dupla sit GE ipsius EH, et agatur per E penes DH linea MEK occurrens ipsis BG, GD apud signa M, K, et secetur EK bifariam in T; quod per doctrinam aequalium momentorum, erit centrum gravitatis trianguli HDG unde sicut in praemissa triangulum HDG solutum a signis B, G, et a solo puncto M appensum iacet, ut nunc est. Itaque aeque repet spatio Z: sed GH ipsius HE, et ideo per 2. sexti Euclidis GB ipsius BM, quare et AB ipsius BM tripla est: igitur, et trigonum DHG spatii Z triplum: quoniam videlicet appensa sunt iis, a quibus pendent, longitudinibus reciproca: quod est propositum.