PROPOSITIO VII.

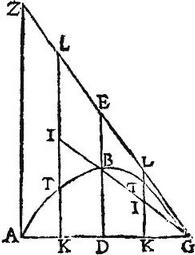
Quibus demonstratis, sit libra ABG, cuius medium B, trigonum autem BDG, rectum habens angulum, qui apud B; suspendatur, a signis B, G; suspendatur quoque, et spatium Z, ex alia parte librae apud A, et aequaliter repat spatium Z apud A suspensum, trigono BDG sic iacenti. Aio quod triplum est trigonum BDG, spatii Z, secetur enim BG in E puncto, itaut dupla sit GE ipsius EB, et agatur penes BD linea EK, quae secetur in aequalia apud T, eritque, ut in libro de Momentis Aequalibus, fuit ostensum, T punctum, centrum gravitatis trigoni BDG: itaque si trigoni BDG, quae quidem secundum B, G appensio solvatur, et suspendatur secundum E, manet trigonum, ut nunc se habet; namque ut in dicto libro ostenditur, recta ET, quae signum appensionis cum centro gravitatis rei appensae connectit, kathetus est ad horizontem, et ideo perpendicularis ad ipsam AG, quae parallelus est horizonti; sic ergo manet trigonum BGD suspensum a signis B, G, sicut suspensum a signo E, et aeque repit spatio Z suspenso a signo A: verum appensa aeque repentitia reciproca sunt spatiis, a quibus pendent: ostensum est enim hoc in momentis aequalibus: igitur sicut quae AB ad lineam BE, sic trigonum BGD ad spatium Z: sed quae AB tripla fuit ipsius BE quoniam BG tripla eiusdem; ergo et trigonum BDG triplum est ipsius Z spatii: quod est propositum.

Contra si triplum sit trigonum BDG ipsius Z spatii, trigonum, et spatium aequaliter repent: quoniam scilicet quae AB tripla ipsius BE: et per doctrinam aequalium momentorum, appensa longitudinis, a quibus pendent, reciproca aeque repunt.