PROPOSITIO XXV.

Si sphaera, et sphaeroides, sive duae sphaeroides figurae communem habentes axem plano secentur ad axem recto; portiones unius erunt portionibus alterius figurae proportionales.

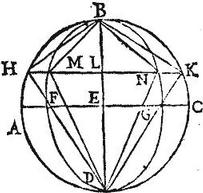
Sit sphaera ABCD, sive sphaeroides; sit enim altera sphaeroides FBGD, quarum axis communis BD, centrumque E; a circulo, et ellipsi, sive ab ellipsibus eiusdem circa dictum axem descriptae; quae secentur plano ad axem recto: cuius cum ellipsibus per axem communis sectio sit linea HMLNK: ita ut factorum in solidis per 17. praemissi, circulorum diametri sint HK, MN in eadem linea. Demonstrandum est, quod abscissae solidorum portiones HBK, HDK sunt portionibus MBN, MDN proportionales hoc modo. Sint circuli, et ellipsis, sive duarum ellipsium solidas figuras describentium secundae diametri AC, FG: intelligantur et coni HBK, MBN communem axem BL, basesque circulos sortiti, quorum diametri HK, MN: cum itaque, per corollarium praecedentem 31. libri de sphaera, et cylindro, et per 20. huius, portio HBK: itemque portio MBN ad conum MBN sit, sicut linea composita ex ED, DL, ad lineam DL; quae est axis relictae maioris portionis in utroque solido; erit permutatim portio HBK ad portionem MBN sicut conus HBK ad conum MBN; sed conus HBK ad conum MBN sicut basis ad basim, et ideo sicut quadratum HL ad quadratum ML; proindeque per 21. primi conicorum, sicut quadratum AE ad quadratum FE, hoc est sicut quadratum AC ad quadratum FG. Quare per 23, huius sic solidum ABCD ad solidum FBGD. Igitur sicut solidum ABCD ad solidum FBGD totum ad totum, sicut portio HBK ad portionem MBN abscissa ad abscissam: ergo per 19. quinti Euclidis erit et portio HDK ad portionem MDN, reliqua ad reliquam, sicut solidum ABCD totum ad solidum FBGD totum; et sicut portio HBK ad portionem MBN abscissa ad abscissam. Et permutatim portio HBK ad portionem HDK sicut portio MBN ad portionem MDN, quod est propositum. [S:269]