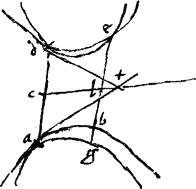
[A:111v] 40a Si hyperbole uni cantrapositarum ad tria puncta coincidat: contraposita ipsius alteri contrapositarum vel non coincidet, vel ad unum tantum coincidet.
Sint contrapositae, quarum non tangentes189 aeb deg. // Itemque aliae duae contrapositae, quarum non tangentes190 zlh tlk. // Hoc pacto, ut tlk coincidat ipsis ged aeb apud m n puncta. // Atque zlh aequidistans primum ipsi aeb coincidat ipsi ged tantum apud x punctum. // Sic fiet ut illae non tangentes191 his non tangentibus192 ad tria tantum puncta m n x coincidant. // Et perinde hyperbole, cuius non tangentes hlk cepta describi intra triangulum xlm tribus in locis coincidet hyperbole, cuius non tangentes193 deb et intra triangulum men deductae. // Sic enim hyperbolarum periferiae, quae secus non tangentes feruntur194, ad totidem puncta coincidunt, ad quot non tangentes earum. // Contrapositae vero earum, quae intra angulos aeg zlt describuntur minime coincident, sicut neque coincidunt non tangentes195 earum, quoniam ea196 lz aequidistare supponuntur. // Quod si ea lz versus partes a z productae coincident: similiter et contrapositarum periferiae coincident ad unum solum punctum: quoniam et ad unum solum tunc coincident ad easdem partes non tangentes197. //
// Verum est ergo, quod infert propositio.