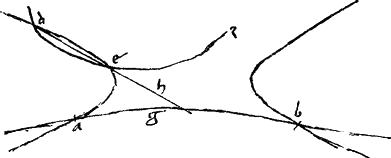
28^a Si ellipsis, vel circulum ad duo puncta tangit idem centrum habens; coniungens tactus per centrum cadit.

[S:141] Tangant se invicem dictae sectiones commune centrum habentes apud a b puncta: // et coniungatur ab. // Dico iam quod ab per centrum venit. // Ducantur enim per a b puncta tangentes sectiones: quae utique aequidistantes erunt. // Coincidant enim, si possibile est, sintque al lb. // Et ab per aequa secetur apud z et coniungatur lz quae, per 29^am secundi Conicorum, diameter erit utriusque sectionis: secetque periferias¹³⁴ apud h m¹³⁵ eatque per centrum sectionum d extra ipsam ab. //¹³⁶ Eritque, per 37^am primi Conicorum, in una sectionum ldz aequale dh in altera vero, aequale dm¹³⁷. // Quare dm¹³⁸ aequale dh. // Quod est impossibile. // Non ergo coincidunt, quae tangunt periferias apud a b. // Aequidistant ergo. // Et perinde, per 27^am 2ⁱ Conicorum, diameter est ab et propterea per centrum transit: // Quod est propositum. Eritque centrum ipsum z punctum: in duo diametri se invicem secant.