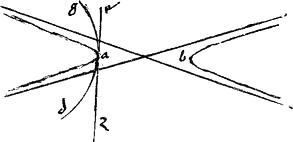
25^a Parabole hyperbolen non tanget ad duo puncta extra ipsam existens.

[S:140] Nam (si possibile est) parabole ahb exterior, hyperbolen amb interiorem tangat apud duo puncta a b. // Et ducantur tangentes utramque sectionem, coincidentesque per 24^am primi¹²⁵ Conicorum ad punctum l ipsae al lb. // Et coniungatur ab quae secetur per medium apud z et coniungatur lz quae, per 29^am secundi Conicorum diameter est utriusque sectionis, secans quidem parabolen apud h et hyperbolen apud m et producta usque ad d ponatur md diameter hyperboles. // Eritque, per 36^am primi Conicorum, ut dz zm sic dl lm. // Maior autem dz quam dl. // Ergo, per 14^am quinti Euclidis et zm maior quam ml et eo magis zh maior, quam hl. // Quod est impossibile: nam per 35 primi Conicorum, aequalis est zh ipsi h¹²⁶ quoniam parabole est ahb diameter autem lz tangensque¹²⁷ la et applicata az. // Restat ergo propositum.