23^a Si praedictarum sectionum quaedem apud duo puncta se tangant invicem, non coincidunt ad aliud.

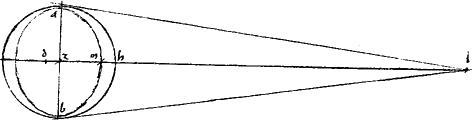
[S:139] Ut si duae sectiones tangant se invicem apud duo puncta a b. // Dico quod alibi nusquam coincidunt. // Si enim possibile est, coincidant apud g et sit prius g punctum extra ipsos a b tactus. // Et ducantur ex a b punctis tangentes: tangent autem utramque sectionem: et coincidant ad l ut in prima descriptione. // Et coniungatur gl secans periferias apud h m ipsamque ab iungentem tactus apud n. // Eritque per 37^am Conicorum, in una quidem sectione, ut gl lh sic gn nh, in altera vero, ut gl lm sic gn nm¹²². // quod est absurdum, sicut in praemissis.

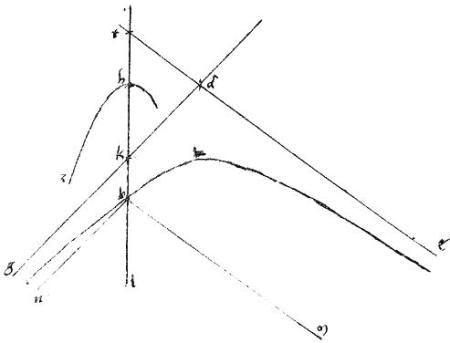
Si autem gh aequidistet tangentibus apud a b puncta (quod in ellipsi et circulo accidere potest) ut in 2^a descriptione: // tunc coniuncta ab per 27^am secundi Conicorum, diameter est sectionis utriusque: et perinde per aequalia secabit tam ipsam gh quam ipsam gm apud n punctum: quod est absurdum.

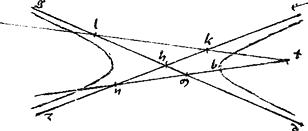
Sit demum g coincidentia inter tactus a b ut in 3^a descriptione: ut scilicet periferiae tangant se invicem apud a b¹²³ secentque apud g punctum. // Ducantur tangentes al lb et coniuncta ab per medium secetur apud z. // Unde, per 29^am secundi Conicorum, lz diameter erit utriusque sectionis. // Quae per punctum g non veniet: sic enim ducta per g penes ab tangeret utramque sectionem per 32^am primi Conicorum: quod est impossibile. // Itaque ducatur per g penes ab linea gchm secans scilicet zl apud c et periferias apud h m. // Eritque in altera sectione gc aequalis ch, in altera autem cg aequalis cm. // Quare cm aequalis ch. // Quod est absurdum.

Similiter autem et si aequidistantes sint tangentes: sequetur idem impossibile, quod in 2^a descriptione: ut in ellipsi et circulo accidit: ducta tunc gchm penes tangentes: et existente ab diametro. // Itaque tangentes se periferiae binis in locis alibi non coincidunt. // Quod est propositum.