21^a Coni sectio vel circulus coni sectionem extrinsecus tangens in uno tantum puncto tangit: intrinsecus vero tangens ad plura puncta, quam duo non tangit.

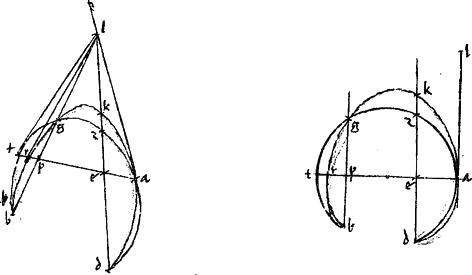
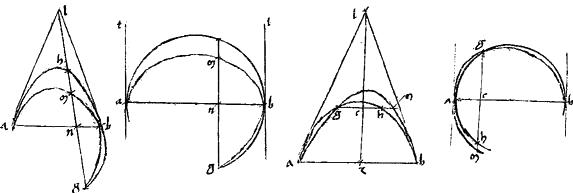
[S:138] Tangat enim, si possibile est, sectio abg¹⁰⁹ sectionem adg extrinsecus apud duo puncta a g. // Et coniungatur recta ag. // Quae aut cadet inter periferias abg adg et sic extra utramque sectionem, quando¹¹⁰ extra¹¹¹ se contingunt. // Quod est impossibile: nam, per 10^am primi Conicorum, intra sectionem cadet¹¹². // Aut ag recta relinquit ex una parte utramque periferiam: et sic extra remotiorem periferiam cadet: // quod per eamdem 10^am est impossibile. // Sectio igitur sectionem extrinsecus ad plura quam unum puncta non tangit.

// Rursum tangat, si possibile est, sectio sectionem, in tribus punctis a b g intrinsecus: // et a punctis a b ducantur tangentes ad db tangent siquidem¹¹³ utramque sectionem. // Et coniungatur ab recta: nec non dg recta, quae secet rectam¹¹⁴ ab apud e punctum: periferias autem apud z h puncta. // Eritque, per 37^am tertii Conicorum, in exteriori sectione quidem, ut gd dh sic ge eh et in interiori, ut gd dz sic ge ez. // Maior autem est gd dh quam gd dz. // Ergo et maior ge eh quam ge ez. // Quare, per 10^am quinti Euclidis ez maior quam eh. // Quod est impossibile. // Sectio igitur sectionem intrinsecus ad plura puncta, quam duo, non tangit. // Quod restabat demonstrandum.

Si autem [[tangentes]]¹¹⁵ apud a b puncta aequidistant, [[...]]¹¹⁶ circulo et ellipsi potest contingere: tunc per 27^am 2ⁱ Conicorum ab diameter erit utriusque sectionis: et perinde secat tam gz quam gh per aequalia apud e. // Quod est absurdum.

Sitque tunc gezh aequidistans [[tangentibus]]¹¹⁷