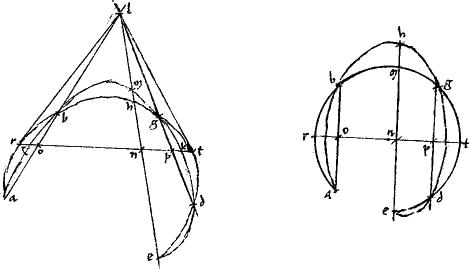
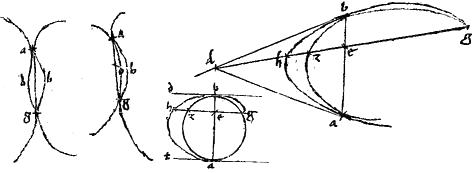
20^a Coni sectio coni sectionem vel circulum non secat ad plura puncta, quam quatuor.

Si enim possibile est, secet ad quinque scilicet a b g d e ita ut in mediis periferiis coincidentia non admittatur. // Et coniunctae ab gd producantur: quae, per 22^am primi Conicorum coincident extra sectiones in parabola et hyperbola, coincidant ad l. // Et sicut est al lb sic sit ao ob; itemque sicut dl lg sic sit dp pg. // Quo fiet ut per 7^am huius, po producta utrinque coincidat utrique sectioni: ut pote periferiis interioribus apud puncta z k exterioribus vero apud puncta r t atque ut ipsae tl lr tangant exteriores periferias: ipsaeque zl lk tangant interiores. // Itaque agatur el secans ipsam op apud n periferiasque apud h m eritque, per 37^am tertii Conicorum, in una sectionum, ut el lh sic en nh atque in altera, sicut el lm sic en nm. // Maior autem¹⁰² el lm quam el lh. // Ergo maior¹⁰³ en nm quam en nh. // Quare, 10^am quinti Euclidis nh maior quam nm. // Quod est impossibile. // Eademque demonstratio circulo et ellipsi accomodabitur, si ab gd productae¹⁰⁴ coincidant. // Si vero aequidistent ab gd in circulo et ellipsi: // secentur bifariam ipsae ab gd apud puncta o p. // Et coniuncta po producatur, et occurrat utrinque periferiis apud t r. // Eritque, per 28^am secundi Conicorum, rt diameter utriusque sectionis. // Ducatur a puncto e quintae sectionis penes ipsas ab gd linea enmh¹⁰⁵ secans quidem diametrum apud n et periferias apud m h eritque, per 47^am primi Conicorum in una quidem sectione en¹⁰⁶ aequalis nm in altera vero en aequalis nh¹⁰⁷. // Quare nh aequalis nm¹⁰⁸. // Quod est impossibile. // Sectiones igitur conicae duae in pluribus, quam quatuor locis se invicem non secant. // Quod fuit demonstrandum.

[A:106v]