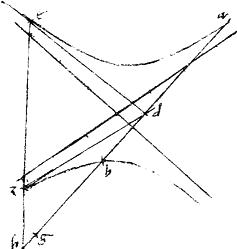
12a Eisdem existentibus sit punctum d intra angulum extrinsecum non tangentium68: sitque sicut ad ![]() db sic ag
db sic ag ![]() gb tunc gz producta coincidet contrapositae sectioni, ut pote apud e punctum, et ed tanget eandem contrapositam.
gb tunc gz producta coincidet contrapositae sectioni, ut pote apud e punctum, et ed tanget eandem contrapositam.
Nam, (si possibile est) producta69 ed tangente et coniuncta ez eat non per g sed per h punctum: // eritque per 39am tertii Conicorum, ut ah ![]() hb sic ad
hb sic ad ![]() db. // Et ideo, sicut ag
db. // Et ideo, sicut ag ![]() gb sic ah
gb sic ah ![]() hb. // Et disiunctim sicut ab
hb. // Et disiunctim sicut ab ![]() bh sic ab
bh sic ab ![]() bg. // Quare per 9am quinti Euclidis gb bh aequales. // Quod est impossibile. // Igitur ez non per aliud, [A:103v] quam g punctum ibit. // Itaque gz coincidit sectioni a apud e punctum: et ed tanget sectionem. // Sicut fuit demonstrandum.
bg. // Quare per 9am quinti Euclidis gb bh aequales. // Quod est impossibile. // Igitur ez non per aliud, [A:103v] quam g punctum ibit. // Itaque gz coincidit sectioni a apud e punctum: et ed tanget sectionem. // Sicut fuit demonstrandum.