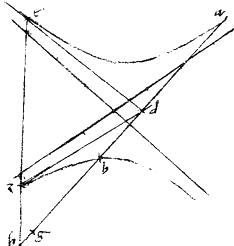
13^a Eisdem existentibus: sit punctum d in una non tangentium⁷⁰: utque ad db⁷¹ sic ag gb: tunc zg aequidistans erit non tangenti⁷², in qua punctum d.

Nam (si possibile est) acta per z punctum penes non tangentem in qua d non veniat per g sed per h punctum. // Eritque, per 36^am tertii Conicorum, ut ad bd sic ah hb. // Quare sicut ah hb sic ag gb. // Et disiunctim, ut ab bg sic ab bh. // Itaque bg bh aequales. // Quod est impossibile. // Igitur, quae per z punctum aequidistat non tangenti⁷³ in qua d punctum, alia non est, quam zg. // Sicut fuit demonstrandum.

SCHOLIUM

Notandum quod hoc in loco theorema quoddam⁷⁴ apparebat simile 11^o75 praecedenti: quippe quod geminabat lineas ductas per punctum d eodem modo sectas: et per terminos earum ductam inferebat coincidere sectioni, et a coincidentiis ad punctum d ductas tangere apud ipsas coincidentias ipsam sectionem. Verum, quoniam eius propositionis demonstratio innititur 36^ae primi Conicorum, quippe quae [A:104r] loquitur de diametro: et per punctum d quod est esxtra centrum, non possunt duci duae diametri: ideo talis demonstratio locum non habet. Et perinde⁷⁶ propositionem ipsam expunximus. Et eamdem ob causam in undecima praemissa linea per punctum d quae secat con[S:135]trapositas per centrum ducendam curavimus: quo 36^a primi, quae illius 11^ae demonstrationi usu venit, locum habeat⁷⁷.