9^a Eisdem existentibus: si punctum d sit in una non tangentium⁵¹, et reliqua eadem sint: ducta per divisiones linea aequidistans erit non tan[S:133]genti, in qua est punctum; et producta coincidet sectioni; et acta a coincidentia ad punctum tanget sectionem.

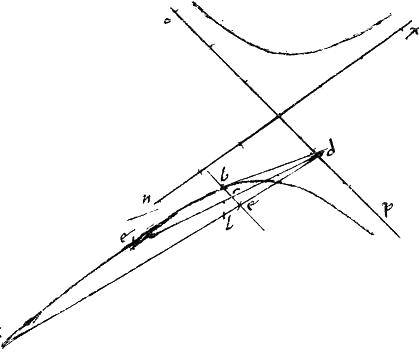
Sit enim hyperbole et non tangentes: // relictumque punctum in altera non tangentium d⁵². // Et ducantur lineae⁵³, et dividantur, ut dictum est⁵⁴. // Et ducatur tangens sectionem db⁵⁵.

// Dico iam quod ducta per b penes ipsam po non tangentem⁵⁶ veniet per puncta c l. // Secus enim veniet vel per alterum ipsorum vel per neutrum. // Veniat per solum c perque punctum e in ipsa zh. // Eritque per 35^am tertii Conicorum, ut zd dh sic ze eh et perinde sicut zl lh. // Quod est absurdum. // Quod si ducta per b aequidistans ipsi po non tangenti, neque per c punctum incedet; absurditas talis geminabitur. // Omnino igitur acta per b ipsi po aequidistans ibit per puncta c l. // Aequidistans itaque erit ipsi po linea cl incidens iam sectioni apud b. // Tangitque bd sectionem. // Verum ergo quod proponitur.