[A:96v] 55a Si contrapositas duae lineae tangentes coincidant: et per concursum ducatur lineae penes tactus coniungentem: a tactibus autem ducantur aequidistantes tangentibus, excitentur autem et a tactibus per unum punctum utriusvis periferiae lineae quae secet aequidistantes; contentum sub abscissis ad quadratum coniungentis tactus rationem habebit eam, quam contentum sub tangentibus ad quadratum ductae per concursum tangentium penes iungentem tactus inter periferias receptae.
336
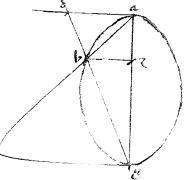
Sint contrapositae abg dez. // Tangentes autem ipsas lineae ahd. // Coniungens tactus ad. // Aequidistans ipsi ad linea ghe. // Aequidistans ipsi dh linea amt. // Aequidistans ipsi ah linea dmn. // Relictum punctum in sectione z. // Per quod agantur azn zdt. // Dico iam quod ut ![]() gh
gh ![]()
![]() ahd sic
ahd sic ![]() ad
ad ![]()
![]() at nd. // Sit enim penes ipsam ad linea zlcb.
337
// Et, quoniam per 20am huius tertii, ut est
at nd. // Sit enim penes ipsam ad linea zlcb.
337
// Et, quoniam per 20am huius tertii, ut est ![]() eh
eh ![]()
![]() hd sic
hd sic ![]()
![]() blz
blz ![]()
![]() dl. // Estque, per 38am secundi Conicorum, eiusque corollarium gh aequalis he. // Et bc lz448. // Ideo iam, ut
dl. // Estque, per 38am secundi Conicorum, eiusque corollarium gh aequalis he. // Et bc lz448. // Ideo iam, ut ![]() gh
gh ![]()
![]() hd sic
hd sic ![]()
![]() czl
czl ![]()
![]() dl. // Est autem, propter similiter sectas, ut
dl. // Est autem, propter similiter sectas, ut ![]() hd
hd ![]()
![]() dha sic
dha sic ![]() dl
dl ![]()
![]() dl ac. // Igitur ex aequali, ut
dl ac. // Igitur ex aequali, ut ![]() gh
gh ![]()
![]() dha sic
dha sic ![]()
![]() czl
czl ![]()
![]() dl ac.
dl ac.
|
|