[A:97r] 56a Si alteram contrapositarum duae lineae tangentes coincidant: per tactus autem aequidistantes ducantur tangentibus: et a tactibus per idem punctum alterius periferiae ducantur lineae, quae secent aequidistantes; contentum tetragonum sub abscissis rationem habebit ad quadratum iungentis tactus compositam ex ea, quam habet connectens concursum tangentium cum puncto medio iungentis tactus, quae est inter punctum medium et alteram periferiam, ad eam, quae est inter eadem periferiam et concursum potentia: et ex ea, quam habet contentum sub tangentibus ad quadratum, quod fit ex dimidia iungentis tactus.
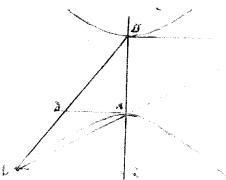
340 Sint contrapositae ab gd. // Quarum centrum o. // Tangentes aezh betc. // Coniungens tactus ab. // Quae per medium secetur apud l. // Et coniuncta le producatur per puncta odx diameter enim erit, per 29am secundi Conicorum. // Ipsi autem ae aequidistans linea bn. // Ipsique be aequidistans linea am. // Et per relictum in altera sectionum punctum g perque tactus a b [A:97v] agantur lineae gan gbm.
|
|
|
|
|
|
TERTII LIBRI CONICORUM APOLLONII
PERGAEI FINIS
Panhormi, hora noctis 2 1/2 quae sequitur diem qui fuit 2um Iunii 1547
Franciscus Maurolycus magno cum labore, vigiliisque correctum scribebat.