|
323
[A:95r] 53a Si in hyperbole, vel ellipsi, vel circulo, vel contrapositis a summitate diametri ducantur ordinate applicatae: et ab eisdem terminis diametri lineae super unum punctum periferiae se invicem secantes vicissim ap[S:125]plicatis inciderint: contentum sub abscissis portionibus applicatarum aequale erit speciei, quae ad eandem diametrum.
324
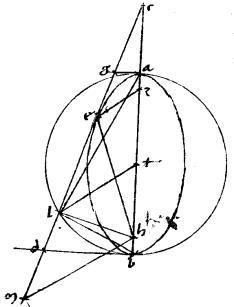
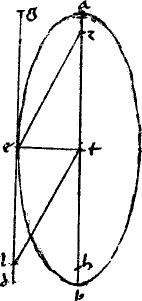
Sit una dictarum sectionum abg. //Cuius diameter ag. // Et ordinate applicentur ad ge. // Et producantur abe dbg. // Dico iam quod   ad eg aequale est speciei, quae ad ag. // Ducatur enim ordinate applicata bz. // Eritque, per 21am primi Conicorum sicut ad eg aequale est speciei, quae ad ag. // Ducatur enim ordinate applicata bz. // Eritque, per 21am primi Conicorum sicut  zb zb   azg sic recta azg sic recta  transversam ag et sicut species, quae ad ag transversam ag et sicut species, quae ad ag   ag.
325
// Quandoquidem dicta species est428 quadrato axis minoris vel diametri coniugatae429: atque recta ag.
325
// Quandoquidem dicta species est428 quadrato axis minoris vel diametri coniugatae429: atque recta  430 axis minor, sive diameter coniugata431 430 axis minor, sive diameter coniugata431  432 ag sint in proportionem continua, per corollarium 13ae vel 15ae primi Conicorum. 432 ag sint in proportionem continua, per corollarium 13ae vel 15ae primi Conicorum. |
|
// Verum per 24am sexti Euclidis ratio  zb zb   azg componitur ex rationibus azg componitur ex rationibus |
|
. |
|
|
|
|
326
// Igitur et ratio speciei   ag componitur ex iisdem ag componitur ex iisdem |
|
. |
|
|
// Sed propter similitudinem triangulorum sicut bz  za sic eg za sic eg  ga. // Itemque sicut bz ga. // Itemque sicut bz  zg sic da zg sic da  ag. ag. |
|
327
// Ergo ratio speciei   ag componetur ex rationibus ag componetur ex rationibus |
|
. |
|
|
Ex quibus per 24am 6i Euclidis componitur ratio  ad eg ad eg   ag. // Quare sicut ag. // Quare sicut   ad eg ad eg   ag sic species ag sic species   ag. // Itaque433 per 9am quinti ag. // Itaque433 per 9am quinti   ad eg aequale434 speciei dictae, quae ad ag435.
328
// Quod est demonstrandum . ad eg aequale434 speciei dictae, quae ad ag435.
328
// Quod est demonstrandum .
|


![]()
![]() ad eg aequale est speciei, quae ad ag. // Ducatur enim ordinate applicata bz. // Eritque, per 21am primi Conicorum sicut
ad eg aequale est speciei, quae ad ag. // Ducatur enim ordinate applicata bz. // Eritque, per 21am primi Conicorum sicut ![]() zb
zb ![]()
![]() azg sic recta
azg sic recta ![]() transversam ag et sicut species, quae ad ag
transversam ag et sicut species, quae ad ag ![]()
![]() ag.
325
// Quandoquidem dicta species est428 quadrato axis minoris vel diametri coniugatae429: atque recta
ag.
325
// Quandoquidem dicta species est428 quadrato axis minoris vel diametri coniugatae429: atque recta ![]() 430 axis minor, sive diameter coniugata431
430 axis minor, sive diameter coniugata431 ![]() 432 ag sint in proportionem continua, per corollarium 13ae vel 15ae primi Conicorum.
432 ag sint in proportionem continua, per corollarium 13ae vel 15ae primi Conicorum.