[A:94v] 318 52a Si in ellipsi ad maiorem axium quadranti speciei aequale comparetur in utramque productum deficiens specie a quadrato424, et a factis ex comparatione punctis ductae lineae in periferia concurrant: ductae simul sumptae aequales erunt axi.
319
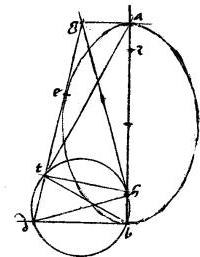
Sit ellipsis, cuius maior axium ab. // Tamque ![]()
![]() agb quam
agb quam ![]()
![]() adb sit quarta pars speciei, quae ad ab. // Et a punctis g d ad periferiam sectionis concurrant ge de. // Dico iam quod ged simul iunctae aequales sunt ab axi. // Ducatur enim tangens tez. // Et a centro sectionis h ipsi ge parallelus ht quae secet ipsam ed apud c.
320
// Et quoniam, per 48am huius, aequalis est angulus gez angulo tec. // Et propter aequidistantiam linearum, angulus gez aequalis angulo etc. // Ideo aequalis erit angulus etc angulo tec. // Quare, per 6am primi Euclidis linea tc aequalis lineae ce. // Et, quoniam ex hypothesim gh aequalis hd et ideo, per 2am sexti Euclidis ec aequalis cd.
321
// Propterea, ed dupla est ipsius ec hoc est ipsius tc. // Sed eg dupla ipsius ch. // Igitur utraque ged dupla ipsius ht. // Fuit autem, per 50am huius ht aequalis ipsi hb. // Ergo ged dupla ipsius hb (quod425 est 1/2 axis ab) et perinde aequalis ipsi ab toti axi. // Quod fuit demonstrandum.
322
// Quod si punctum e sit in medio periferiae, hoc est apud extremum axis minoris: tunc facilius sequitur demonstratio ex additione 50ae huius. // Namque in eo casu eg gd426 sunt aequales et eg aequalis th quae fuit aequalis ipsi hb per additionem praedictam. // Quare rursum ged simul aequales427 toti ab sicut proponitur.
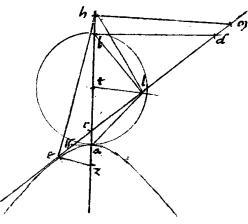
adb sit quarta pars speciei, quae ad ab. // Et a punctis g d ad periferiam sectionis concurrant ge de. // Dico iam quod ged simul iunctae aequales sunt ab axi. // Ducatur enim tangens tez. // Et a centro sectionis h ipsi ge parallelus ht quae secet ipsam ed apud c.
320
// Et quoniam, per 48am huius, aequalis est angulus gez angulo tec. // Et propter aequidistantiam linearum, angulus gez aequalis angulo etc. // Ideo aequalis erit angulus etc angulo tec. // Quare, per 6am primi Euclidis linea tc aequalis lineae ce. // Et, quoniam ex hypothesim gh aequalis hd et ideo, per 2am sexti Euclidis ec aequalis cd.
321
// Propterea, ed dupla est ipsius ec hoc est ipsius tc. // Sed eg dupla ipsius ch. // Igitur utraque ged dupla ipsius ht. // Fuit autem, per 50am huius ht aequalis ipsi hb. // Ergo ged dupla ipsius hb (quod425 est 1/2 axis ab) et perinde aequalis ipsi ab toti axi. // Quod fuit demonstrandum.
322
// Quod si punctum e sit in medio periferiae, hoc est apud extremum axis minoris: tunc facilius sequitur demonstratio ex additione 50ae huius. // Namque in eo casu eg gd426 sunt aequales et eg aequalis th quae fuit aequalis ipsi hb per additionem praedictam. // Quare rursum ged simul aequales427 toti ab sicut proponitur.