[S:124] 314 51a Si hyperboles, vel contrapositarum ad axim aequale quadranti speciei comparetur excedens specie a quadrato419 in utrasque productum: et a factis punctis ex comparatione ducantur lineae ad punctum unum in utravis sectionum; maior minorem excedet axi.
315
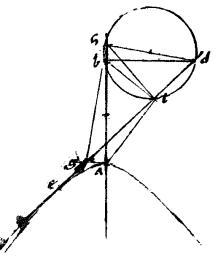
Sit enim hyperbole, vel contrapositae. // Quarum axis ab. // Centrum autem g. // Sitque tam ![]()
![]() adb quam
adb quam ![]() aeb quadrans speciei, quae ad ab. // Et ad quodvis punctum relictum utriusvis sectionis, utpote ad420 punctum z sectionis az ducantur ez zd. // Dico iam quod ez excedit ipsam zd in axe ab. // Hoc est quod ez aequalis est ipsis zd ab simul sumptis.
316
// Ducatur enim zct tangens sectionem apud z. // Et aequidistans ipsi zd ipsa tgh. // Eruntque anguli cth czd coalterni aequales et, per 48am huius, anguli czd hzt aequales. // Quare anguli hzt cth421 aequales. // Et ideo, per 6am primi422 Euclidis linea hz aequalis ipsi ht.
317
// Sed ez dupla423 ipsius zh et ideo dupla est ipsius ht. // Atque, per praecedentem, gt aequalis ipsi gb. // Igitur ez dupla utriusque hg gb. // Sed ipsius hg est ipsa zd dupla: itemque ipsius gb dupla ipsa ab. // Ergo ez aequalis est ipsis zd ab pariter acceptis. // Quod fuit demonstrandum.
aeb quadrans speciei, quae ad ab. // Et ad quodvis punctum relictum utriusvis sectionis, utpote ad420 punctum z sectionis az ducantur ez zd. // Dico iam quod ez excedit ipsam zd in axe ab. // Hoc est quod ez aequalis est ipsis zd ab simul sumptis.
316
// Ducatur enim zct tangens sectionem apud z. // Et aequidistans ipsi zd ipsa tgh. // Eruntque anguli cth czd coalterni aequales et, per 48am huius, anguli czd hzt aequales. // Quare anguli hzt cth421 aequales. // Et ideo, per 6am primi422 Euclidis linea hz aequalis ipsi ht.
317
// Sed ez dupla423 ipsius zh et ideo dupla est ipsius ht. // Atque, per praecedentem, gt aequalis ipsi gb. // Igitur ez dupla utriusque hg gb. // Sed ipsius hg est ipsa zd dupla: itemque ipsius gb dupla ipsa ab. // Ergo ez aequalis est ipsis zd ab pariter acceptis. // Quod fuit demonstrandum.