5a Si contrapositas duae lineae tangentes coincidant, et relictum sit in utravis sectionum punctum quoddam18 et ab ipso ducantur duae lineae, haec quidem penes tangentem, illa vero penes tactus coniungentem; factum sub ipsis triangulum ad ductam diametrum per concursum tangentium differt a recepto triangulo ad concursum tangentium per receptum triangulum ad tangentem et ductam per tactum diametrum.
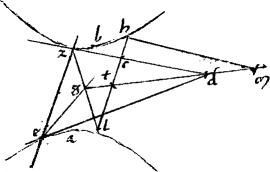
15 Sint contrapositae a b. // Quarum centrum g. // Tangentes ed, dz. // Et coniungant19 e, z puncta tactuum. // Et gd producatur. // Et zg, eg coniunctae producantur. // Et relictum sit in sectione quoddam20 punctum h per quod ducantur penes ipsam quidem ez ipsa quidem hctl incidens quidem ipsi dz apud c ipsi autem gd apud t ipsique zg apud l at vero penes ipsam dz tangentem ipsam hm occurrens ipsi gd productae apud m. 16 // Dico iam quod triangulum htm aequale est triangulo ctd una cum triangulo czl. // Namque, per 39am et 38am praecedentis libri, ipsa gd diameter est contrapositarum, ad quam ordinata est ipsa ez. // Cum ergo hm ipsi zd tangenti et hl ipsi ez ordinatae aequidistet21 iam per 45am primi [A:66v] Conicorum triangulum htm aequale est triangulis tlg, gdz simul sumptis hoc est ipsis iam triangulis tdc, czl simul. 17 // Quod iam est demonstrandum.