292 45^a Si in hyperbole, vel ellipsi, vel circulo, vel contrapositis, ab extremitatibus axis excitentur lineae ad rectos: et quadrati speciei aequale rectangulum ad axim comparetur, in hyperbole quidem et contrapositis excedens specie a quadrato³⁹⁸, in ellipsi, et circulo deficiens: ducatur autem quaedam linea tangens sectionem et concurrens excitatis ad rectos: ductae a concursibus lineae ad utrumvis punctorum in axi ex comparatione factum rectum angulum facient.

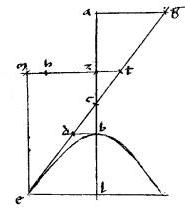
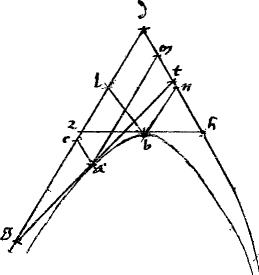
293 [S:121] Sit una dictarum sectionum, cuius axis ab. // Cui ad rectos sint ag bd. // Tangens ged. // Punctum tactus e. // Sitque tam azb quam ahb quarta pars speciei ad ab deficiens quidem in ellipsi et circulo, excedens autem in hyperbole. // Et coniungantur gz zd itemque dh hg. // Dico iam quod tam gzd quam ghd angulus rectus est. // Nam, cum, per 42^am praecedentem ag bd sit quadrans speciei ad ab. 294 // Atque per hypothesim azb sit quadrans³⁹⁹ eiusdem. // Iam aequalia sunt ag bd ⁴⁰⁰ azb. // Quare per 15^am sexti Euclidis ut ga az sic zb bd. // Sed anguli apud a b recti per hypothesim. // Igitur per 4^am sexti gaz aequiangulum ⁴⁰¹ zbd. // Unde angulus agz aequalis est angulo bzd. 295 // Et quoniam rectus gaz⁴⁰² ideo ipsi anguli agz azg aequales uni recto. // Quare et anguli [A:91v] bzd azg aequales uni recto. // Omnes autem tres anguli azg gzd dzb⁴⁰³ simul faciunt duos rectos per 14^am primi Euclidis //. Superest ergo angulus gzd rectus. // Similiter omnino et angulus ghd rectus arguetur. 296 // Quod est demonstrandum.