289 44a Si hyperbolen, vel contrapositas duae lineae tangentes coincidant non tangentibus; quae puncta concursuum connectunt, aequidistantes sunt iungenti tactus.
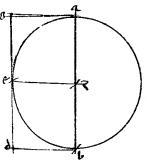
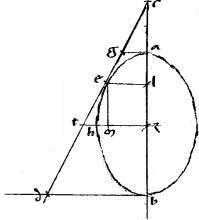
// Sit hyperbole, vel contrapositae ab. // Non tangentes gde. // Tangentes gatz ebth. // Tactus a b. // Et coniungantur ab eg zh.
290
// Dico iam quod ab eg zh aequidistantes sunt. // Cum enim per corollarium praecedentis, ![]()
![]() gdz aequale sit
gdz aequale sit ![]() hde iam per 15am sexti Euclidis erit, ut gd
hde iam per 15am sexti Euclidis erit, ut gd ![]() de sic dh
de sic dh ![]() dz. // Igitur, per 2am sexti, aequidistat ge ipsi zh. // Quare ex similitudine
dz. // Igitur, per 2am sexti, aequidistat ge ipsi zh. // Quare ex similitudine ![]()
![]() tge tzh sicut tz
tge tzh sicut tz ![]() zg sic th
zg sic th ![]() he ut autem gz
he ut autem gz ![]() za sic eh
za sic eh ![]() hb dupla397 enim utraque utriusque, per 3am 2i Conicorum.
291
// Ex aequo igitur, ut tz
hb dupla397 enim utraque utriusque, per 3am 2i Conicorum.
291
// Ex aequo igitur, ut tz ![]() za sic th
za sic th ![]() hb. // Ergo triangula tab tzh similia, et perinde, ex aequalitate angulorum coalternorum zh aequidistat ab. // Sed ostensum est, [A:91r] quod ge aequidistat zh. // Itaque omnes tres ab eg zh aequidistat. // Quemadmodum proponitur demonstrandum.
hb. // Ergo triangula tab tzh similia, et perinde, ex aequalitate angulorum coalternorum zh aequidistat ab. // Sed ostensum est, [A:91r] quod ge aequidistat zh. // Itaque omnes tres ab eg zh aequidistat. // Quemadmodum proponitur demonstrandum.