42a Si hyperbole, vel ellipsi, vel circulo, vel contrapositis ab extremis diametri ducantur ordinate applicatae: et alia quaedam ut contingit tangens sectionem agatur; tangens abscindet ab applicatis lineas, sub quibus contentum tetragonum est quadrans speciei diametro adiacentis.
281
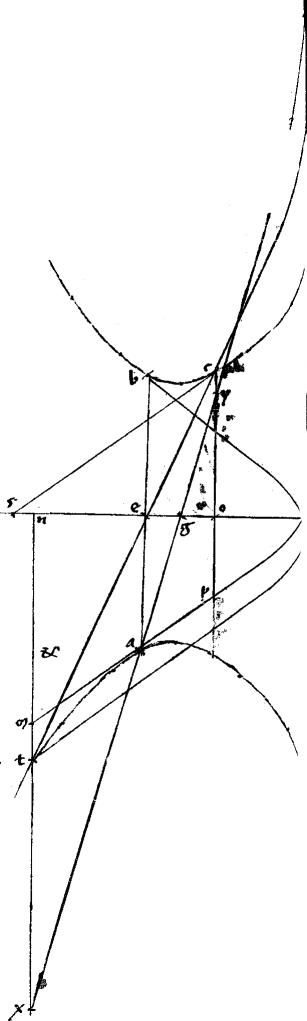
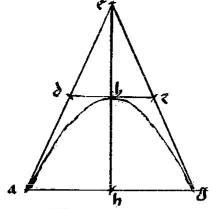
Sit enim quaevis dictarum sectionum be. // Cuius diameter ab. // Centrum z. // Ad extrema diametri applicatae ag bd. // Tangens ged. // Punctum tactus e. // Dico iam quod ![]()
![]() ag bd quadrans est speciei ad ab. // Nam, si zh coniugata ipsi ab diametro in ellipsi et circulo per e punctum it: tunc, per additam 32ae primi, aequidistabit dg ipsi ab et perinde ag zh bd sunt aequales quare tunc
ag bd quadrans est speciei ad ab. // Nam, si zh coniugata ipsi ab diametro in ellipsi et circulo per e punctum it: tunc, per additam 32ae primi, aequidistabit dg ipsi ab et perinde ag zh bd sunt aequales quare tunc ![]() 387 ag bd est ipsum
387 ag bd est ipsum ![]() zh388 quod est quadrans speciei ad ab quandoquidem per 13am vel 15am primi Conicorum, tota diameter, quae [A:90r] dupla est ipsius zh possit389 totam speciem diametri ab.
282
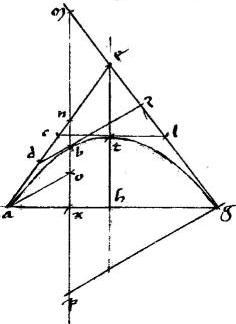
// Quare tunc manifesta est propositio. // Sed iam zh non veniat per e punctum tunc autem per 24am et 25am primi Conicorum, deg tangens coincidet ba diametro. // Coincidat ad c. // Et zh concurrat tangenti apud t. // Sintque el ipsi zh. // Et em ipsi ab aequidistantes. // Quibus peractis, quoniam, per 37am primi Conicorum,
zh388 quod est quadrans speciei ad ab quandoquidem per 13am vel 15am primi Conicorum, tota diameter, quae [A:90r] dupla est ipsius zh possit389 totam speciem diametri ab.
282
// Quare tunc manifesta est propositio. // Sed iam zh non veniat per e punctum tunc autem per 24am et 25am primi Conicorum, deg tangens coincidet ba diametro. // Coincidat ad c. // Et zh concurrat tangenti apud t. // Sintque el ipsi zh. // Et em ipsi ab aequidistantes. // Quibus peractis, quoniam, per 37am primi Conicorum, ![]()
![]() czl aequale est
czl aequale est ![]() az. Ideo per 15am sexti Euclidis erit, ut cz
az. Ideo per 15am sexti Euclidis erit, ut cz ![]() za sic za
za sic za ![]() zl.
283
// Et conversim, ut az
zl.
283
// Et conversim, ut az ![]() zc sic lz
zc sic lz ![]() za. // Et coniunctim, ut ac
za. // Et coniunctim, ut ac ![]() cz sic la
cz sic la ![]() az sive zb. // Et permutatim390, ut ca
az sive zb. // Et permutatim390, ut ca ![]() al sic cz
al sic cz ![]() zb. // Et rursus conversim, ut la
zb. // Et rursus conversim, ut la ![]() ac sic bz
ac sic bz ![]() zc. // Et rursus coniunctim391 ut lc
zc. // Et rursus coniunctim391 ut lc ![]() ca sic bc
ca sic bc ![]() cz. // Propter similitudinem autem triangulorum est ut lc
cz. // Propter similitudinem autem triangulorum est ut lc ![]() ca sic le
ca sic le ![]() ag. // Utque bc
ag. // Utque bc ![]() cz sic bd
cz sic bd ![]() zt.
284
Igitur ut bd
zt.
284
Igitur ut bd ![]() zt sic el
zt sic el ![]() ga. // Quare, per 15am sexti Euclidis
ga. // Quare, per 15am sexti Euclidis ![]()
![]() bd ga aequale est
bd ga aequale est ![]() zt el hoc est
zt el hoc est ![]() tzm. // Sed, per 38am primi Conicorum
tzm. // Sed, per 38am primi Conicorum ![]()
![]() tzm aequale est
tzm aequale est ![]() zh hoc est quadrans392 speciei ad ab. // Ergo et
zh hoc est quadrans392 speciei ad ab. // Ergo et ![]()
![]() bd ga quadrans est eiusdem speciei. // Quod fuit demonstrandum.
bd ga quadrans est eiusdem speciei. // Quod fuit demonstrandum.