271 41a Si parabolen tres lineae tangentes coincidant invicem: ad eandem rationem secabuntur.
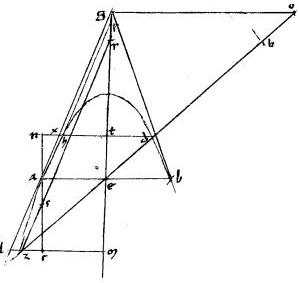
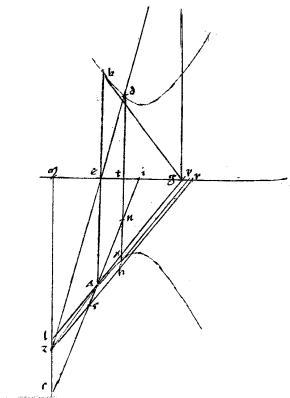
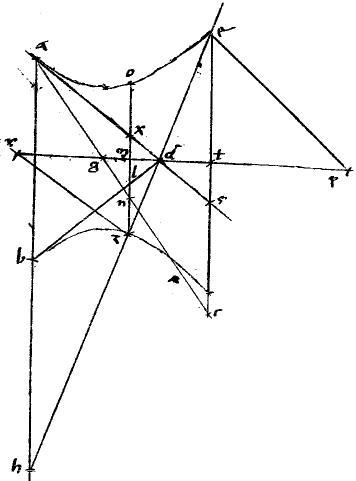
Sit parabole abg. // Tangentes autem ade ezg dbz. // Tactuum puncta a b g. // Dico iam quod est, ut gz ![]() ze sic ed
ze sic ed ![]() da et sic zb
da et sic zb ![]() bd.
272
// Coniungatur enim ag et secetur per medium apud h. // Et ducatur eh quae, per 29am secundi Conicorum, diameter erit sectionis. // Si igitur eh incedat per b tactum iam per 5am praedicti dbz aequidistat ipsi ag et ah applicata est ipsi ebh diametro.
273
// Quare per 35am primi Conicorum eb aequalis bh et per 2am sexti Euclidis gz aequalis ze item ed aequalis da nec non zb aequalis bd in quo casu manifestum est propositum. // Sed iam diameter eh non veniat per b sed per t punctum. // Et ducatur per t penes ipsam ag linea ctl quae, per 32am primi Conicorum, tanget sectionem apud t.
274
// Quare tunc per eadem, quae prius, ac erit aequalis ce atque el aequalis lg. // Ducatur per b penes eh ipsa mnboxp. // Per puncta vero a g ipsae ao gp aequidistantes ipsi dbz. // Quoniam igitur mb aequidistat eh diametro, diameter est, per 46am primi Conicorum ad quam ipsae dbz ao gp ordinate applicatae sunt. // Sed gm tangens. //
275
Ergo, per 35am primi mb aequalis bp et per 2am 6i Euclidis mz aequalis zg. // Fuit et el aequalis lg. // Igitur, ut mg
bd.
272
// Coniungatur enim ag et secetur per medium apud h. // Et ducatur eh quae, per 29am secundi Conicorum, diameter erit sectionis. // Si igitur eh incedat per b tactum iam per 5am praedicti dbz aequidistat ipsi ag et ah applicata est ipsi ebh diametro.
273
// Quare per 35am primi Conicorum eb aequalis bh et per 2am sexti Euclidis gz aequalis ze item ed aequalis da nec non zb aequalis bd in quo casu manifestum est propositum. // Sed iam diameter eh non veniat per b sed per t punctum. // Et ducatur per t penes ipsam ag linea ctl quae, per 32am primi Conicorum, tanget sectionem apud t.
274
// Quare tunc per eadem, quae prius, ac erit aequalis ce atque el aequalis lg. // Ducatur per b penes eh ipsa mnboxp. // Per puncta vero a g ipsae ao gp aequidistantes ipsi dbz. // Quoniam igitur mb aequidistat eh diametro, diameter est, per 46am primi Conicorum ad quam ipsae dbz ao gp ordinate applicatae sunt. // Sed gm tangens. //
275
Ergo, per 35am primi mb aequalis bp et per 2am 6i Euclidis mz aequalis zg. // Fuit et el aequalis lg. // Igitur, ut mg ![]() gz sic eg
gz sic eg ![]() gl. [A:89v] // Et permutatim, ut mg
gl. [A:89v] // Et permutatim, ut mg ![]() ge sic zg
ge sic zg ![]() gl sed propter similitudinem triangulorum ut mg
gl sed propter similitudinem triangulorum ut mg ![]() ge sic xg
ge sic xg ![]() gh. // Igitur, ut zg
gh. // Igitur, ut zg ![]() gl sic et xg
gl sic et xg ![]() gh.
276
// Ut autem hg
gh.
276
// Ut autem hg ![]() ga sic lg
ga sic lg ![]() ge dimidium siquidem utrumque utriusque. // Ex aequo igitur, ut zg
ge dimidium siquidem utrumque utriusque. // Ex aequo igitur, ut zg ![]() ge sic xg
ge sic xg ![]() ga. // Et conversim eg
ga. // Et conversim eg ![]() gz sic ag
gz sic ag ![]() gx. // Et disiun[S:119]ctim, sicut ez
gx. // Et disiun[S:119]ctim, sicut ez ![]() zg sic ax
zg sic ax ![]() xg. // Et conversim, gz
xg. // Et conversim, gz ![]() ze sicut gx
ze sicut gx ![]() xa.
277
// Rursus, quoniam diameter est mb tangens autem an et applicata ao ideo, per 45am primi Conicorum, aequalis est nb ipsi bo et per 2am sexti Euclidis nd aequalis da est autem et ec aequalis ca. // Igitur, ut ea
xa.
277
// Rursus, quoniam diameter est mb tangens autem an et applicata ao ideo, per 45am primi Conicorum, aequalis est nb ipsi bo et per 2am sexti Euclidis nd aequalis da est autem et ec aequalis ca. // Igitur, ut ea ![]() ac sic na
ac sic na ![]() ad. // Et permutatim, ut ea
ad. // Et permutatim, ut ea ![]() an sic ca
an sic ca ![]() ad. // Sed, ut ea
ad. // Sed, ut ea ![]() an sic ha
an sic ha ![]() ax propter similitudinem triangulorum.
278
// Igitur, ut ca
ax propter similitudinem triangulorum.
278
// Igitur, ut ca ![]() ad sic ha
ad sic ha ![]() ax. // Est autem ut ga
ax. // Est autem ut ga ![]() ah sic ea
ah sic ea ![]() ac dupla siquidem utraque utriusque. // Ex aequo igitur, ut ga
ac dupla siquidem utraque utriusque. // Ex aequo igitur, ut ga ![]() ax sic ea
ax sic ea ![]() ad. // Et disiunctim, sicut gx
ad. // Et disiunctim, sicut gx ![]() xa sic ed
xa sic ed ![]() da.
279
// Demum quoniam, ob similitudinem triangulorum ut gx
da.
279
// Demum quoniam, ob similitudinem triangulorum ut gx ![]() xa sic gp
xa sic gp ![]() ao ut autem gp
ao ut autem gp ![]() ao sic zb
ao sic zb ![]() bd (quandoquidem dimidia duplis proportionalia, namque zb 1/2 ipsius gp quoniam bm386 1/2 ipsius mp. // Et bd 1/2 ipsius ao sicut bn 1/2 ipsius no). Idcirco, et zb
bd (quandoquidem dimidia duplis proportionalia, namque zb 1/2 ipsius gp quoniam bm386 1/2 ipsius mp. // Et bd 1/2 ipsius ao sicut bn 1/2 ipsius no). Idcirco, et zb ![]() bd sicut gx
bd sicut gx ![]() xa.
280
// Ostensum est ergo, quod gz
xa.
280
// Ostensum est ergo, quod gz ![]() ze atque ed
ze atque ed ![]() da nec non zb
da nec non zb ![]() bd se habet sicut gx
bd se habet sicut gx ![]() xa hoc est eamdem habet rationem. // Quod fuit demonstrandum.
xa hoc est eamdem habet rationem. // Quod fuit demonstrandum.