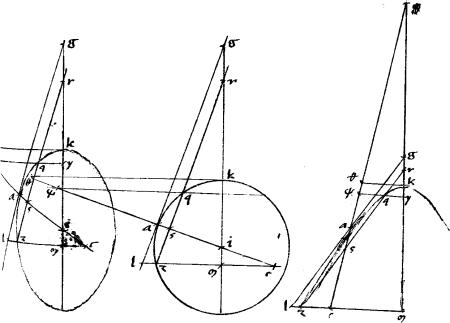
40^a Iisdem existentibus: si per concursum tangentium ducatur linea penes tactus iungentem: et a medio puncto iungentis tactus excitata linea secet utramque periferiam incidens in aequidistantem iungenti tactus; erit, ut tota excitata ad extra receptam inter aequidistantem et periferiam, sic factae ipsius portiones a medio puncto ad periferias.

266 Sint contrapositae a b. // Centrum g. // Tangentes adb. // Coniungens tactus ab. // Producta dg secet, per 39^am 2ⁱ ipsam ab per medium apud e. // Et per d concursum aequidistans ab ducatur zdhlq. // Per e autem utcumque excitetur tecl secans quidem periferias apud t c occurrensque ipsi zdhlq apud l. // Dico iam quod est ut tl lc sic te ec. 267 // Ducantur enim per puncta t c aequidistantes ipsi ab ipsae xtmn cyop. Aequidistantes autem ipsi ad ipsae tr cs. // Et ducatur xagq. // Eritque, propter similitudinem et proportionem triangulorum ut xa ay sic ma ap atque te ec propter similiter sectas et tn co. 268 // Itaque ut tn co sic ma ap ³⁸² trn cso itemque sic xma ayp propter similitudinem [S:118] et proportionem figurarum.

// Sed per 5am huius trn aequale xma mnd 383 simul.

Itemque cos aequale ayp dop simul.

Igitur ut xma simul ayp mnd dop simul totum videlicet ad totum

sic xma ayp ablatum ad ablatum. 269 Quare³⁸⁴ per 19^am quinti sic etiam erit mnd dop reliquum scilicet³⁸⁵ ad reliquum. // Verum propter proportionem figurarum ut xma ayp sic xa ay. [A:89r] Et similiter, ut mnd dop sic mn op. // Ergo et ut mn op sic xa ay. 270 // Propter proportionem autem similiter sectarum, ut mn op sic nd od utque xa ay sic te ec utque nd od sic tl lc. // Quam ob rem ut tl lc sic te ec et ideo,ut tl lc sic te ec. // Quod erat demonstrandum.