[A:88r] 260 39^a Si contrapositas duae lineae tangentes coincidant, et per tactus linea producatur: et per concursum tangentium ducta linea secet utran[S:117]que periferiam et coniungentem tactus; erit, ut tota ducta ad extra receptam inter periferiam et coniungentem tactus; sic factae portiones lineae a periferiis ad concursum tangentium.

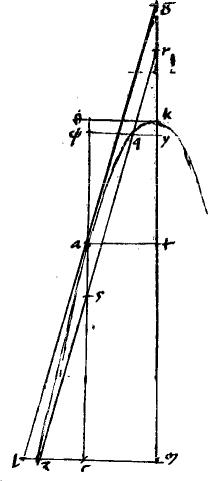
261 Sint contrapositae a b. // Centrum g. // Tangentes adb. // Coniunctae ab gd producatur. // Et per d concursum tangentium agatur linea edzh secans periferias apud e z occurensque ipsi ab apud h. // Dico iam quod est ut eh hz sic ed dz. // Coniungatur enim ag et incidat ipsi etsc ductae penes ab apud c punctum. // Item penes ab sit ipsa znlmxo. 262 // Penes autem ad ipsae ep zr occurentes ipsi gd productae apud p r puncta. // Eritque propter aequidistantiam linearum et similitudinem triangulorum sicut et ts sic zm mx. // Et permutatim, ut et zm sic ts mx. // Quare, sicut et zm sic ts mx. // Et etp zmr et dts dmx propter proportionem figurarum.

263 // Sed per 5am huius etp aequale asc tds .

Itemque zmr aequale axn dmx .

Igitur erit, ut dts dmx sic asc lrang axn dts dmx simul

hoc est totum ad totum, ut ablatum ad ablatum. // Quare per 19^am 5ⁱ ut dts dmx ablatum³⁸¹ ad ablatum, sic iam et asc anx reliquum scilicet ad reliquum. 264 // Sed propter similitudinem et proportionem triangulorum ut asc anx sic ca an hoc est propter proportionem similiter sectarum linearum sic eh hz. // Propter proportionem autem figurarum similiter ut dts dmx sic td dm hoc est ob proportionem laterum similium triangulorum sic ed dz. // Ergo sicut ed dz sic eh hz. // Quam ob rem, et sicut eh hz sic ed dz. 265 // Quod fuerat demonstrandum.

[A:88v]