[A:87v] 256 38a Iisdem existentibus: si per concursum tangentium ducatur quaedam linea penes iungentem tactus: et per medium punctum iungentis tactus acta secet periferiam ad duo puncta occurrens in aequidistantem iungenti tactus; erit, ut acta tota ad extra receptam inter periferiam et aequidistantem, sic factae portiones a iungente tactus.
257
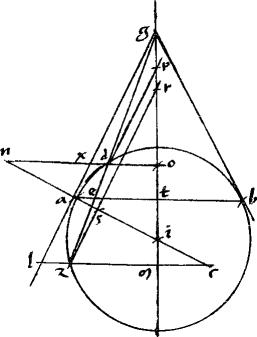
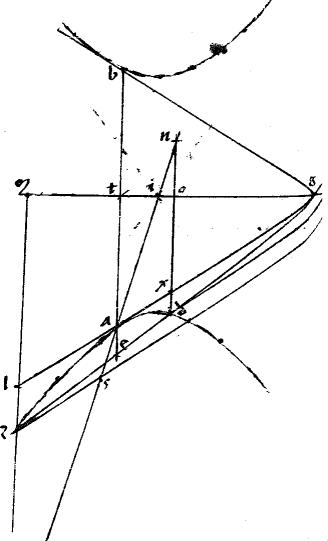
Sit ab sectio, vel sectiones. // Tangentes agb. // Iungens tactus ab. // Diametri an mg. // Ipsa quidem gm diameter per 30am378 et 39am secundi Conicorum, per medium secabit ipsam ab secet apud e punctum. // Ipsa go aequidistans ipsi ab. // Ducatur per e punctum linea zedo secans periferiam vel periferias apud z d occurrensque ipsi go apud o. // Dico iam quod sicut est zo ![]() od sic ze
od sic ze ![]() ed.
258
// Ducatur enim aequidistantes ipsi ab lineae lzcm dthxn aequidistantes autem ipsi lg ipsae zr hp. // Quibus peractis, non aliter, quam in praecedenti, ostendemus, quod est, sicut
ed.
258
// Ducatur enim aequidistantes ipsi ab lineae lzcm dthxn aequidistantes autem ipsi lg ipsae zr hp. // Quibus peractis, non aliter, quam in praecedenti, ostendemus, quod est, sicut ![]() lm
lm ![]()
![]() xt sic
xt sic ![]() la
la ![]()
![]() ax et sic
ax et sic ![]() lg
lg ![]()
![]() gx atque
gx atque ![]() zo
zo ![]()
![]() od. // Quandoquidem fuit ibi, ut lg
od. // Quandoquidem fuit ibi, ut lg ![]() gx sic zg
gx sic zg ![]() gd propter similitudinem triangulorum. // Ut autem
gd propter similitudinem triangulorum. // Ut autem ![]() la
la ![]()
![]() ax sic
ax sic ![]() ze
ze ![]()
![]() ed ex proportione linearum.
259
// Ut igitur
ed ex proportione linearum.
259
// Ut igitur ![]() ze
ze ![]()
![]() ed sic
ed sic ![]() zo
zo ![]()
![]() od. // Quare sicut zo
od. // Quare sicut zo ![]() od sic ze
od sic ze ![]() ed. //Quod fuit demonstrandum.
ed. //Quod fuit demonstrandum.
Scholium379
Huc [[...]]380 descriptio hyperboles, ellipseos et circuli, quae omittutur, quoniam facile patent ex ipsa paraboles descriptione: hoc excepto quod in parabola diametri aequidistant, in caeteris ad centrum coincidunt.