37a Si coni sectionem, vel circuli periferiam, vel contrapositas duae lineae tangentes coincidant: et a coincidentia366 in lineam tactus ipsarum iungentem ducatur quaedam secans periferiam ad duo puncta; erit, ut tota ad extra receptam, sic factae portiones a iungente tactus.
247
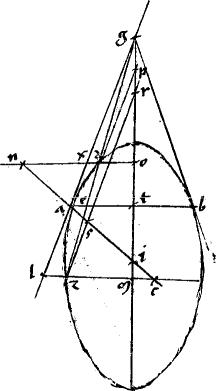
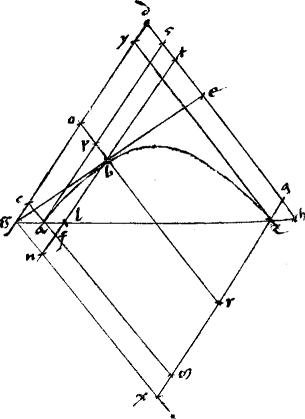
Sit coni sectio ab. // Tangentes agb. // Coniungens tactus ab. // Linea gdez secans periferiam sectionis apud d z puncta: ipsamque ab apud e. // Dico iam quod est, sicut zg ![]() gd sic ze
gd sic ze ![]() ed. // Ducantur enim diametri sectionis gprotm nac in parabola quidem aequidistantes; in hyperbola, vero ellipsi, circulo, contrapositisque ad centrum i concurrentes.
248
// Item zr dp aequidistantes ipsi lag. // Nec non lzcm nxdo aequidistantes ipsi aetb tactus iungenti. // Eritque propter similitudinem triangulorum ut zg
ed. // Ducantur enim diametri sectionis gprotm nac in parabola quidem aequidistantes; in hyperbola, vero ellipsi, circulo, contrapositisque ad centrum i concurrentes.
248
// Item zr dp aequidistantes ipsi lag. // Nec non lzcm nxdo aequidistantes ipsi aetb tactus iungenti. // Eritque propter similitudinem triangulorum ut zg ![]() gd sic lz
gd sic lz ![]() xd et sic zm
xd et sic zm ![]() do et sic lm
do et sic lm ![]() xo. // Igitur ut
xo. // Igitur ut ![]() lm
lm ![]()
![]() xo sic
xo sic ![]() zm
zm ![]()
![]() do et propter similitudinem et proportionem figurarum sic
do et propter similitudinem et proportionem figurarum sic ![]() lmg
lmg ![]()
![]() xog et sic
xog et sic ![]() 367 zrm
367 zrm ![]()
![]() dpo totum scilicet ad totum sicut ablatum ad ablatum.
249
// Quare, per 19am quinti Euclidis sic
dpo totum scilicet ad totum sicut ablatum ad ablatum.
249
// Quare, per 19am quinti Euclidis sic ![]() lgrz
lgrz ![]()
![]() xgpd reliquum videlicet ad reliquum. // Aequale autem
xgpd reliquum videlicet ad reliquum. // Aequale autem ![]() lgrz
lgrz ![]() lo alc in parabola, quidem hyperbola, circulo et ellipsi, ut ostendit scholium adiectum: in contrapositis autem per 11am huius. // Item aequale
lo alc in parabola, quidem hyperbola, circulo et ellipsi, ut ostendit scholium adiectum: in contrapositis autem per 11am huius. // Item aequale ![]() xgpd
xgpd ![]() lo anx in parabola videlicet, hyperbola, ellipsi, circuloque, per 2am huius: in contrapositis vero, per corollarium 11ae huius.
250
// Igitur, ut
lo anx in parabola videlicet, hyperbola, ellipsi, circuloque, per 2am huius: in contrapositis vero, per corollarium 11ae huius.
250
// Igitur, ut ![]() lm
lm ![]()
![]() xo sic
xo sic ![]() alc
alc ![]()
![]() anx. // Verum propter similitudinem triangulorum ut
anx. // Verum propter similitudinem triangulorum ut ![]() lm
lm ![]()
![]() xo sic
xo sic ![]() zg
zg ![]()
![]() gd. // Et propter proportionem figurarum, ut
gd. // Et propter proportionem figurarum, ut ![]() alc
alc ![]()
![]() anx sic
anx sic ![]() la
la ![]()
![]() ax et sic
ax et sic ![]() ze
ze ![]()
![]() ed. // Itaque, ut
ed. // Itaque, ut ![]() zg
zg ![]()
![]() gd sic
gd sic ![]() ze
ze ![]()
![]() ed. // Et, quoniam proportionalium quadratorum proportionalia sunt latera; ideo iam, et ut zg
ed. // Et, quoniam proportionalium quadratorum proportionalia sunt latera; ideo iam, et ut zg ![]() gd sic ze
gd sic ze ![]() ed.
251
// Quod proponebatur demonstrandum. [A:86v]
ed.
251
// Quod proponebatur demonstrandum. [A:86v]
[[![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ]]370
]]370
[[![]()
![]()
![]()
![]()
![]()
![]() ]]371
]]371
252
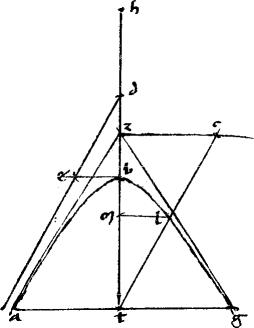
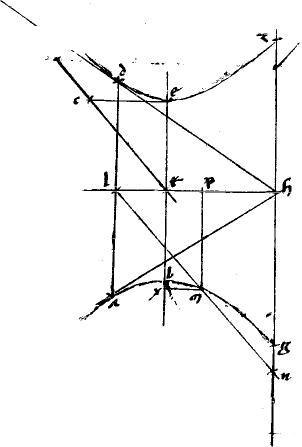
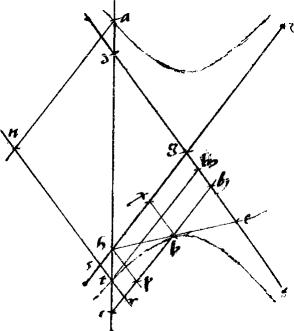
Superest nunc,ad complementum demonstrationis huius 37ae ostendere quod aequale est ![]() alc ipsi
alc ipsi ![]() lgrz.
lgrz.
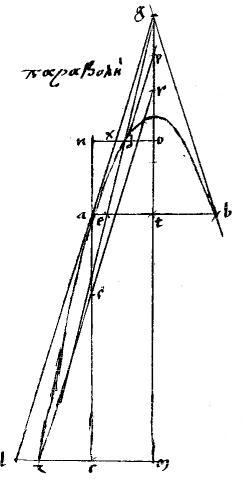
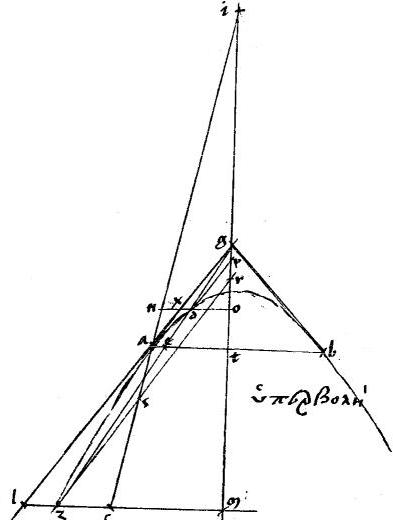
Assumens375 itaque ipsius propositionis lineamenta exclusis lineis gdez nxdo aetb gb quae huiuc demonstrationi minime usu venientes, lectorem perturbarent. // Duco k![]() tangentem apud k et occurrentem ipsi ca diametro apud
tangentem apud k et occurrentem ipsi ca diametro apud ![]() .
253
// Secet autem zr periferiam apud q et ipsi k
.
253
// Secet autem zr periferiam apud q et ipsi k![]() aequidistantem duco
aequidistantem duco ![]() q y. // Ipsamque zq secet ac diameter apud s. // Secabit autem bifariam in parabola quidem per 46am primi Conicorum, in caeteris, per 47am eiusdem. // Quo fit, ut
q y. // Ipsamque zq secet ac diameter apud s. // Secabit autem bifariam in parabola quidem per 46am primi Conicorum, in caeteris, per 47am eiusdem. // Quo fit, ut ![]()
![]() s c z s
s c z s![]() q iam similia sunt et invicem aequilatera, et aequalia. //
254
Triangulum s
q iam similia sunt et invicem aequilatera, et aequalia. //
254
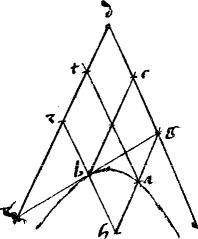
Triangulum s![]() q aequale est
q aequale est ![]() sagr in parabola quidem, per 42am primi Conicorum: in ceteris autem, per demonstrata in 47a eiusdem376 // Igitur et
sagr in parabola quidem, per 42am primi Conicorum: in ceteris autem, per demonstrata in 47a eiusdem376 // Igitur et ![]() scz aequale erit377 eidem
scz aequale erit377 eidem ![]() sagr. // Commune apponatur
sagr. // Commune apponatur ![]() lasz. // Et conflabitur totum
lasz. // Et conflabitur totum ![]() alc aequale iam toti
alc aequale iam toti ![]() lgrz.
255
// Quod quidem restabat demonstrandum. // Quod si varia punctorum et linearum positio casum variaret: adhuc accomodanda esset casui lineatio: lectorisque solertia adhibenda: incredibile enim memoratu est, quam variae descriptiones cuivis apolloniano theoremati sint necessariae.
lgrz.
255
// Quod quidem restabat demonstrandum. // Quod si varia punctorum et linearum positio casum variaret: adhuc accomodanda esset casui lineatio: lectorisque solertia adhibenda: incredibile enim memoratu est, quam variae descriptiones cuivis apolloniano theoremati sint necessariae.