240 36a Iisdem existentibus; si a relicto puncto ducta linea neque sectionem secet ad duo puncta, neque aequidistans sit non tangenti, coincidat autem contrapositae sectioni; erit quidem, [A:85v] ut tota ad eam, quae est inter sectionem et aequidistantem per tactum; sic, quae inter contrapositam et non tangentem ad eam, quae inter non tangentem et alteram sectionem.
241
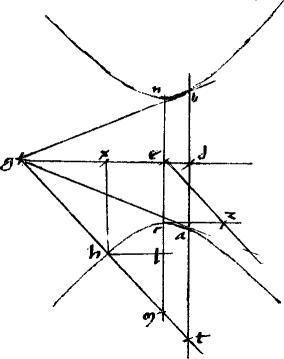
Sint contrapositae a b. // Centrum g. // Non tangentes dge zgh359. // In ipsa gh relictum punctum h. // Tangens hbe. // Tactus b. // Linea hd neque aequidistans ge neque sectionem secans ad duo puncta: quae, per 16am 2i Conicorum, coincidet utrique sectionum a b ut pote ad puncta d t360.
242
// Linea bcl aequidistans gh et occurrens ipsi ht productae apud c. // Dico iam quod ut ac ![]() ct sic ah
ct sic ah ![]() ht. // Ducantur enim aequidistantes ipsi gh ipsae tm an aequidistantes autem ipsa361 ge ipsae bx hp rtsn. // Et, quoniam, per 16am secundi Conicorum ad aequalis ipsi ht. // Et propter similitudinem et proportionem triangulorum ut ah
ht. // Ducantur enim aequidistantes ipsi gh ipsae tm an aequidistantes autem ipsa361 ge ipsae bx hp rtsn. // Et, quoniam, per 16am secundi Conicorum ad aequalis ipsi ht. // Et propter similitudinem et proportionem triangulorum ut ah ![]() ht sic ns
ht sic ns ![]() st.
243
Itemque, ut dt
st.
243
Itemque, ut dt ![]() th sic gs
th sic gs ![]() sh. // Idcirco ut ns
sh. // Idcirco ut ns ![]() st sic gs
st sic gs ![]() sh. // Sed, per primam sexti Euclidis ut ns
sh. // Sed, per primam sexti Euclidis ut ns ![]() st sic
st sic ![]() nsg
nsg ![]()
![]() gst. Itemque, ut gs
gst. Itemque, ut gs ![]() sh sic
sh sic ![]() gsr
gsr ![]()
![]() hsr362. // Igitur, ut
hsr362. // Igitur, ut ![]() nsg
nsg ![]()
![]() gst sic
gst sic ![]() gsr
gsr ![]()
![]() hsr.
hsr.
|
|